题目内容
已知二次函数f(x)=ax2+bx+c(a≠0)满足条件f(-x+5)=f(x-3),f(2)=0,且方程f(x)=x有两个相等实根.问是否存在实数m、n(m<n)使得f(x)的定义域为[m,n]时,值域为[3m,3n].如果存在,求出m、n的值;如果不存在,请说明理由.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)根据已知条件分别列出三个方程联立求得a和b和c的值.
(2)对n≤1,m≥1和m<1,n>1进行分类通论,根据二次函数的图象找到函数的最大值和最小值表达式,联立方程求得m和n进行验证.
(2)对n≤1,m≥1和m<1,n>1进行分类通论,根据二次函数的图象找到函数的最大值和最小值表达式,联立方程求得m和n进行验证.
解答:
解:(1)∵f(-x+5)=f(x-3),
∴函数的对称轴方程x=-
=1,①,
f(2)=4a+2b+c=0,②,
∵方程f(x)=x有两个相等实根.
∴对于f(x)-x=ax2+(b-1)x+c=0,△=(b-1)2-4ac=0,③
联立①②③求得a=-
,b=1,c=0,
∴f(x)=-
x2+x,
(2)①当n≤1时,函数f(x)在[m,n]单调减,则
,求得n=-4,m=-4,(与m<n矛盾)或n=12,m=-20,与n≤1矛盾,
②当m≥1时,函数f(x)在[m,n]单调增,则
,求得n=0或n=-4,均不符合题意,
同理当m<1,n>1时,3m=-
+1,m=
,
令f(m)=-
×
+
=
=3n,求得n<1,不符合题意,
令f(n)=-
n2+n=3n,求得n=0或-4,与n>1矛盾,
综合可知不存在这样的n和m,
∴函数的对称轴方程x=-
| b |
| 2a |
f(2)=4a+2b+c=0,②,
∵方程f(x)=x有两个相等实根.
∴对于f(x)-x=ax2+(b-1)x+c=0,△=(b-1)2-4ac=0,③
联立①②③求得a=-
| 1 |
| 2 |
∴f(x)=-
| 1 |
| 2 |
(2)①当n≤1时,函数f(x)在[m,n]单调减,则
|
②当m≥1时,函数f(x)在[m,n]单调增,则
|
同理当m<1,n>1时,3m=-
| 1 |
| 2 |
| 1 |
| 6 |
令f(m)=-
| 1 |
| 2 |
| 1 |
| 36 |
| 1 |
| 6 |
| 11 |
| 72 |
令f(n)=-
| 1 |
| 2 |
综合可知不存在这样的n和m,
点评:本题主要考查了二次函数的性质.考查了学生的数形结合思想和分类讨论思想的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 黑白两种颜色的正方形地砖依照如图的规律拼成若干个图形,现将一粒豆子随机撒在第10个图中,则豆子落在白色地砖上的概率是( )
黑白两种颜色的正方形地砖依照如图的规律拼成若干个图形,现将一粒豆子随机撒在第10个图中,则豆子落在白色地砖上的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
数列{an}满足a1=
,an+1=1-
,那么a10=( )
| 1 |
| 2 |
| 1 |
| an |
| A、-1 | ||
B、
| ||
| C、1 | ||
| D、2 |
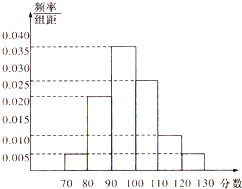 我校高1201、1202、1203、1204四个班,从中随机抽取部分学生进行成绩统计,各班被抽取学生的人数恰好成等差数列,人数最少的班被抽取了24人,抽取的学生的测试成绩统计结果整理得如图所示频率分布直方图,其中分数在[120,130]的人数为6人.
我校高1201、1202、1203、1204四个班,从中随机抽取部分学生进行成绩统计,各班被抽取学生的人数恰好成等差数列,人数最少的班被抽取了24人,抽取的学生的测试成绩统计结果整理得如图所示频率分布直方图,其中分数在[120,130]的人数为6人.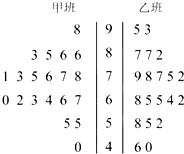 某次月考从甲、乙两班中各抽取20个物理成绩,整理数据得到茎叶图如图所示,根据茎叶图解决下列问题.
某次月考从甲、乙两班中各抽取20个物理成绩,整理数据得到茎叶图如图所示,根据茎叶图解决下列问题.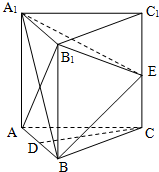 如图,在三棱柱ABC-A1B1C1中,每个侧面均为边长为2的正方形,D为底边AB的中点,E为侧棱CC1的中点.
如图,在三棱柱ABC-A1B1C1中,每个侧面均为边长为2的正方形,D为底边AB的中点,E为侧棱CC1的中点.