题目内容

8．某数学兴趣小组有3名男生和2名女生，从中任选出2名同学参加数学竞赛，那么对立的两个事件是（　　）
A．恰有1名男生与恰有2名女生B．至少有1名男生与全是男生
C．至少有1名男生与至少有1名女生D．至少有1名男生与全是女生

分析 互斥事件是两个事件不包括共同的事件，对立事件首先是互斥事件，再就是两个事件的和事件是全集，由此规律对四个选项逐一验证即可得到答案．

解答 解：选取的两名学生一男一女时，恰有1名男生和恰有2女生，故A个事件是互斥事件，但不是对立事件；
选取两名学生均为男生时，至少有1名男生和全是男生同时发生，故B个事件不是互斥事件，更不可能是对立事件；
选取的两名学生一男一女时，至少有1名男生和至少有1名女生，故C个事件不是互斥事件，更不可能是对立事件；
至少有1名男生和全是女生，两个事件不可能同时发生，且两个事件的和事件是全集，故D中两个事件是对立事件，
故选：D

点评 本题考查互斥事件与对立事件，解题的关键是理解两个事件的定义及两事件之间的关系．属于基本概念型题．

练习册系列答案
相关题目
18．若实数x，y，m满足|x-m|＞|y-m|，则称x比y远离m．
（Ⅰ）比较log20.6与20.6哪一个远离0；
（Ⅱ）已知函数f（x）的定义域$D=\left\{{x\left|{x≠\frac{kπ}{2}+\frac{π}{4}，k∈Z}\right.}\right\}$，任取x∈D，f（x）等于sinx和cosx中远离0的那个值，写出函数f（x）的解析式以及f（x）的三条基本性质（结论不要求证明）．
19．已知两条不同的直线m，n和两个不同的平面α，β，给出下面四个命题：
①若m∥α，n∥β，且α∥β，则m∥n；
②若m∥α，n⊥β，且α⊥β，则m∥n；
③若m⊥α，n∥β，且α∥β，则m⊥n；
④若m⊥α，n⊥β，且α⊥β，则m⊥n；
其中正确的个数有（　　）
A．4B．3C．2D．1
16．已知全集为R，集合A={x|x2-2x＞0}，B={x|1＜x＜3}，则∁RB=（-∞，1]∪[3，+∞），A∩B=（2，3）．
3．已知直线l的方程为mx-y+1-m=0，圆C的方程为x2+（y-1）2=5．
（Ⅰ）证明：直线l与圆C相交；
（Ⅱ）设直线l与圆C交于两点A，B，求弦AB的中点M的轨迹方程．
13．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{3}x，x＞0}\\{f（x+1），x＜0}\end{array}\right.$，则f（-$\frac{8}{9}$）=-2．
20．大气能见度和雾霾、降雨等天气情况密切相关，而大气能见度直接影响车辆的行车速度V（千米/小时）和道路的车流密度M（辆/千米），经有关部门长时间对某道路研究得出，大气能见度不足100米时，为保证安全，道路应采取封闭措施，能见度达到100米后，车辆的行车速度V和大气能见度x（米）近似满足函数V（x）$\left\{\begin{array}{l}{\frac{1}{10}x+10，100≤x＜800}\\{90，x≥800}\end{array}\right.$，已知道路的车流密度M（辆/千米）是大气能见度x（米）的一次函数，能见度为100时，车流密度为160；当能见度为500时，车流密度为为80．
（1）当x≥100时，求道路车流密度M与大气能见度x的函数解析式；
（2）当车流量F（x）的解析式（车流量=行车速度×车流密度）；
（3）当大气能见度为多少时，车流密度会达到最大值，并求出最大值．
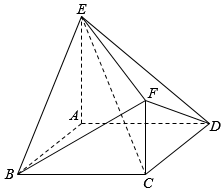17．如图，已知多面体ABCDEF中，ABCD为菱形，∠ABC=60°，AE⊥平面ABCD，AE∥CF，AB=AE=1，AF⊥BE．
（Ⅰ）求证：平面BAF⊥平面BDE；
（Ⅱ）求二面角B-AF-D的余弦值．
18．若函数f（x）=ax3-2x2在x=-1时取得极值，则f（1）等于（　　）
A．-$\frac{10}{3}$B．-$\frac{2}{3}$C．0D．$\frac{1}{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网