题目内容
13.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}x,x>0}\\{f(x+1),x<0}\end{array}\right.$,则f(-$\frac{8}{9}$)=-2.分析 由-$\frac{8}{9}$<0知f(-$\frac{8}{9}$)=f(-$\frac{8}{9}$+1)=f($\frac{1}{9}$),从而求解.
解答 解:由分段函数知,
f(-$\frac{8}{9}$)=f(-$\frac{8}{9}$+1)
=f($\frac{1}{9}$)
=log3$\frac{1}{9}$=-2,
故答案为:-2.
点评 本题考查了分段函数的简单应用,注意自变量的值的范围即可.

练习册系列答案
相关题目
3.若集合A={1,a,b},B={1,-1,2},且B=A,则a+b的值为( )
| A. | 3 | B. | 1 | C. | 0 | D. | 不能确定 |
1.已知y=excosx,则( )
| A. | y′=-exsinx | B. | y′=ex-sinx | C. | y′=$\sqrt{2}$exsin(x+$\frac{π}{4}$) | D. | y′=$\sqrt{2}$exsin($\frac{π}{4}$-x) |
8.某数学兴趣小组有3名男生和2名女生,从中任选出2名同学参加数学竞赛,那么对立的两个事件是( )
| A. | 恰有1名男生与恰有2名女生 | B. | 至少有1名男生与全是男生 | ||
| C. | 至少有1名男生与至少有1名女生 | D. | 至少有1名男生与全是女生 |
2.如图是一个几何体的三视图,则这个几何体的表面积是( )
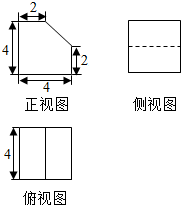

| A. | 84 | B. | $76+8\sqrt{2}$ | C. | $78+8\sqrt{2}$ | D. | $80+8\sqrt{2}$ |
3.在空间在,设m,n,l是三条不同的直线,α,β是两个不同的平面,则下列命题中正确的是( )
| A. | 若m⊥l,n⊥l,则m∥n | B. | 若m∥α,n∥α,则m∥n | C. | 若m⊥α,m⊥β,则α∥β | D. | 若m∥α,m∥β,则α∥β |