题目内容
20.大气能见度和雾霾、降雨等天气情况密切相关,而大气能见度直接影响车辆的行车速度V(千米/小时)和道路的车流密度M(辆/千米),经有关部门长时间对某道路研究得出,大气能见度不足100米时,为保证安全,道路应采取封闭措施,能见度达到100米后,车辆的行车速度V和大气能见度x(米)近似满足函数V(x)$\left\{\begin{array}{l}{\frac{1}{10}x+10,100≤x<800}\\{90,x≥800}\end{array}\right.$,已知道路的车流密度M(辆/千米)是大气能见度x(米)的一次函数,能见度为100时,车流密度为160;当能见度为500时,车流密度为为80.(1)当x≥100时,求道路车流密度M与大气能见度x的函数解析式;
(2)当车流量F(x)的解析式(车流量=行车速度×车流密度);
(3)当大气能见度为多少时,车流密度会达到最大值,并求出最大值.
分析 (1)利用待定系数法求道路车流密度M与大气能见度x的函数解析式;
(2)根据题意,函数F(x)表达式为分段函数的形式;
(3)由(2),分段求最值,即可得出结论.
解答 解:(1)设道路车流密度M与大气能见度x的函数解析式为M(x)=kx+b,
由题意,$\left\{\begin{array}{l}{100k+b=160}\\{500k+b=80}\end{array}\right.$,∴k=-$\frac{1}{5}$,b=180,
∴M(x)=-$\frac{1}{5}$x+180,x≥100;
(2)∵车流量=行车速度×车流密度,
∴F(x)=$\left\{\begin{array}{l}{(\frac{1}{10}x+10)(-\frac{1}{5}x+180)=-\frac{1}{50}{x}^{2}+16x+1800,100≤x<800}\\{90(-\frac{1}{5}x+180)=-18x+16200,x≥800}\end{array}\right.$;
(3)当100≤x<800时,F(x)=-$\frac{1}{50}$(x-400)2+5000,
当x=400时,其最大值为5000,
当x≥800时,F(x)=-18x+16200为减函数,
∴当x=800时,其最大值为1800.
综上,当大气能见度为400米时,车流密度会达到最大值,最大值为5000辆/小时.
点评 本题给出车流密度的实际问题,求车流密度最大值及相应的车流密度,着重考查了函数、最值等基础知识,同时考查运用数学知识解决实际问题的能力,属于中档题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
10.设函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x},x<0}\\{lo{g}_{\frac{1}{2}}x,x≥0}\end{array}\right.$,则f(log2$\frac{1}{6}$)+f($\frac{1}{2}$)的值等于( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 5 | D. | 7 |
11.设l、m、n为不同的直线,α、β为不同的平面,有如下四个命题,其中正确命题的个数是( )
①若α⊥β,l⊥α,则l∥β
②若α⊥β,l?α,则l⊥β
③若l⊥m,m⊥n,则l∥n
④若m⊥α,n∥β且α∥β,则m⊥n.
①若α⊥β,l⊥α,则l∥β
②若α⊥β,l?α,则l⊥β
③若l⊥m,m⊥n,则l∥n
④若m⊥α,n∥β且α∥β,则m⊥n.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
8.某数学兴趣小组有3名男生和2名女生,从中任选出2名同学参加数学竞赛,那么对立的两个事件是( )
| A. | 恰有1名男生与恰有2名女生 | B. | 至少有1名男生与全是男生 | ||
| C. | 至少有1名男生与至少有1名女生 | D. | 至少有1名男生与全是女生 |
12.若集合M={x|x>2},n={x|1<x≤3},则N∩(∁RM)等于( )
| A. | (1,2] | B. | [-2,2] | C. | (1,2) | D. | [2,3] |
9.如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2014}$的值的一个程序框图,则判断框内可填入的条件是( )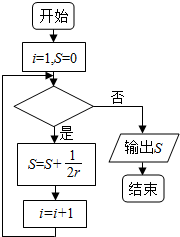

| A. | i≤1006 | B. | i≤1007 | C. | i>1007 | D. | i>1006 |