题目内容
18.若函数f(x)=ax3-2x2在x=-1时取得极值,则f(1)等于( )| A. | -$\frac{10}{3}$ | B. | -$\frac{2}{3}$ | C. | 0 | D. | $\frac{1}{3}$ |
分析 对函数求导,因为x=-1是极值点,则该处导数为0,故可求出a的值,即可求出f(1).
解答 解:由已知得f′(x)=3ax2-4x,
又因为在x=-1处有极值,
所以f′(-1)=0,
即3a+4=0,即a=-$\frac{4}{3}$,
所以f(1)=-$\frac{4}{3}$-2=-$\frac{10}{3}$.
故选:A.
点评 本题考查了极值点处的性质,即极值点处导数为零,据此列出a的方程求解,属基础题.

练习册系列答案
相关题目
8.某数学兴趣小组有3名男生和2名女生,从中任选出2名同学参加数学竞赛,那么对立的两个事件是( )
| A. | 恰有1名男生与恰有2名女生 | B. | 至少有1名男生与全是男生 | ||
| C. | 至少有1名男生与至少有1名女生 | D. | 至少有1名男生与全是女生 |
9.如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2014}$的值的一个程序框图,则判断框内可填入的条件是( )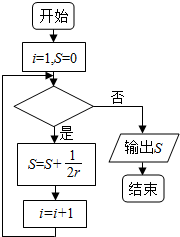

| A. | i≤1006 | B. | i≤1007 | C. | i>1007 | D. | i>1006 |
3.在空间在,设m,n,l是三条不同的直线,α,β是两个不同的平面,则下列命题中正确的是( )
| A. | 若m⊥l,n⊥l,则m∥n | B. | 若m∥α,n∥α,则m∥n | C. | 若m⊥α,m⊥β,则α∥β | D. | 若m∥α,m∥β,则α∥β |
8.若x∈(1,a),则M=logax2,N=loga2x的大小关系是( )
| A. | M<N | B. | M>N | C. | M=N | D. | 不能确定 |