题目内容
19.已知两条不同的直线m,n和两个不同的平面α,β,给出下面四个命题:①若m∥α,n∥β,且α∥β,则m∥n;
②若m∥α,n⊥β,且α⊥β,则m∥n;
③若m⊥α,n∥β,且α∥β,则m⊥n;
④若m⊥α,n⊥β,且α⊥β,则m⊥n;
其中正确的个数有( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 根据空间直线,平面平行和垂直的判定定理分别进行判断即可.
解答 解:①若m∥α,n∥β,则m与n没有关系;故①错误,
②若α⊥β,当m∥α,则m∥β或m?β,若n⊥β,则m⊥n;故②错误,
③若m⊥α,α∥β,则m⊥β,n∥β,则m⊥n成立;故③正确,
④若m⊥α,α⊥β,则m∥β或m?β,若n⊥β,则m⊥n成立;故④正确,
故正确是③④,
故选:C
点评 本题主要考查命题的真假判断,涉及空间直线和平面平行和垂直以及平面和平面垂直和平行的判定,要求熟练掌握相应的判定定理和性质定理.

练习册系列答案
相关题目
9.已知F是抛物线y2=2x的焦点,准线与x轴的交点为M,点N在抛物线上,且|MN|=2|NF|,则∠FMN等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
10.设函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x},x<0}\\{lo{g}_{\frac{1}{2}}x,x≥0}\end{array}\right.$,则f(log2$\frac{1}{6}$)+f($\frac{1}{2}$)的值等于( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 5 | D. | 7 |
7.下列个选项中,关于两个变量所具有的相关关系描述正确的是( )
| A. | 圆的面积与半径具有相关性 | B. | 纯净度与净化次数不具有相关性 | ||
| C. | 作物的产量与人的耕耘是负相关 | D. | 学习成绩与学习效率是正相关 |
14.某研究机构对高二学生的记忆力x和判断力y进行统计分析,给出变量x、y的6组数据如表:
由表中数据得出线性回归方程y=$\widehat{b}$x+$\widehat{a}$的斜率为$\widehat{b}$=3.3.当x=12时,预测y的值为( )
| x | 3 | 4 | 5 | 6 | 8 | 10 |
| y | 40 | 45 | 60 | 55 | 70 | 90 |
| A. | 79.8 | B. | 96.6 | C. | 83.1 | D. | 69.7 |
11.设l、m、n为不同的直线,α、β为不同的平面,有如下四个命题,其中正确命题的个数是( )
①若α⊥β,l⊥α,则l∥β
②若α⊥β,l?α,则l⊥β
③若l⊥m,m⊥n,则l∥n
④若m⊥α,n∥β且α∥β,则m⊥n.
①若α⊥β,l⊥α,则l∥β
②若α⊥β,l?α,则l⊥β
③若l⊥m,m⊥n,则l∥n
④若m⊥α,n∥β且α∥β,则m⊥n.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
8.某数学兴趣小组有3名男生和2名女生,从中任选出2名同学参加数学竞赛,那么对立的两个事件是( )
| A. | 恰有1名男生与恰有2名女生 | B. | 至少有1名男生与全是男生 | ||
| C. | 至少有1名男生与至少有1名女生 | D. | 至少有1名男生与全是女生 |
9.如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2014}$的值的一个程序框图,则判断框内可填入的条件是( )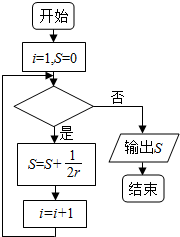

| A. | i≤1006 | B. | i≤1007 | C. | i>1007 | D. | i>1006 |