题目内容
某研究性学习小组对昼夜温差与某种子发芽数的关系进行研究,他们分别记录了四天中每天昼夜温差与每天100粒种子浸泡后的发芽数,得到如下资料:
(1)求这四天浸泡种子的平均发芽率;
(2)有这样一个研究项目,在这四天中任选两天,记发芽的种子数分别为m,n(m<n),请以(m,n)的形式列出所有的基本事件,记事件A为“m,n满足
”,求事件A发生的概率.
| 时间 | 第一天 | 第二天 | 第三天 | 第四天 |
| 温差(℃) | 9 | 10 | 8 | 11 |
| 发芽(粒) | 33 | 39 | 26 | 46 |
(2)有这样一个研究项目,在这四天中任选两天,记发芽的种子数分别为m,n(m<n),请以(m,n)的形式列出所有的基本事件,记事件A为“m,n满足
|
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)可得发芽总数为:33+39+26+46=144,可得平均发芽率;
(2)列出的总的基本事件有:(26,33),(26,39),(26,46),(33,39),(33,46),(39,46)共6个,事件A包括(33,46),(39,46)共2个,由概率公式可得.
(2)列出的总的基本事件有:(26,33),(26,39),(26,46),(33,39),(33,46),(39,46)共6个,事件A包括(33,46),(39,46)共2个,由概率公式可得.
解答:
解:(1)由题意可得四天的发芽总数为:33+39+26+46=144,
∴这四天浸泡种子的平均发芽率为:
×100%=36%;
(2)∵任选两天种子的发芽数为m,n,且m<n,
∴列出的总的基本事件有:(26,33),(26,39),(26,46),
(33,39),(33,46),(39,46)总共6个,
事件A包括(33,46),(39,46)共2个,
∴P(A)=
=
∴这四天浸泡种子的平均发芽率为:
| 144 |
| 400 |
(2)∵任选两天种子的发芽数为m,n,且m<n,
∴列出的总的基本事件有:(26,33),(26,39),(26,46),
(33,39),(33,46),(39,46)总共6个,
事件A包括(33,46),(39,46)共2个,
∴P(A)=
| 2 |
| 6 |
| 1 |
| 3 |
点评:本题考查古典概型的概率求解,列举是解决问题的关键,属基础题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
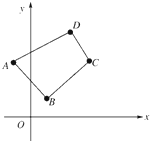 已知四点坐标:A(-1,3),B(1,1),C(4,4),D(3,5).
已知四点坐标:A(-1,3),B(1,1),C(4,4),D(3,5).