题目内容
已知-
<α<0,sinα=-
.
(1)求tanα的值;
(2)求cos2α+sin(
-α)的值.
| π |
| 2 |
| 4 |
| 5 |
(1)求tanα的值;
(2)求cos2α+sin(
| π |
| 2 |
考点:二倍角的余弦
专题:三角函数的求值
分析:(1)由条件利用同角三角函数的基本关系,求得tanα的值.
(2)利用诱导公式、二倍角公式化简所给的式子,可得结果.
(2)利用诱导公式、二倍角公式化简所给的式子,可得结果.
解答:
解:(1)因为-
<α<0,sinα=-
,故cosα=
,所以tanα=-
.
(2)cos2α+sin(
-α)=1-2sin2α+cosα=1-
+
=
.
| π |
| 2 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 3 |
(2)cos2α+sin(
| π |
| 2 |
| 32 |
| 25 |
| 3 |
| 5 |
| 8 |
| 25 |
点评:本题主要考查同角三角函数的基本关系,诱导公式、二倍角公式的应用,属于基础题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
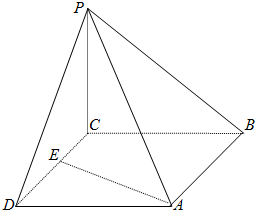 如图,四棱锥P-ABCD的底面为正方形,平面PCD⊥平面ABCD,平面PBC⊥平面ABCD,E为线段CD上任意一点(不包括端点).
如图,四棱锥P-ABCD的底面为正方形,平面PCD⊥平面ABCD,平面PBC⊥平面ABCD,E为线段CD上任意一点(不包括端点).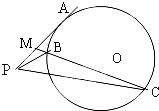 如图,PA是圆O的切线,切点为A,过PA的中点M作割线交圆O于点B和C.
如图,PA是圆O的切线,切点为A,过PA的中点M作割线交圆O于点B和C.