题目内容
已知函数f（x）=Asin（x+
），x∈R，且f（
）=
（1）求A的值；
（2）若角θ的终边与单位圆的交于点P（
，
），求f（
-θ）．
| π |
| 3 |
| 5π |
| 12 |
3
| ||
| 2 |
（1）求A的值；
（2）若角θ的终边与单位圆的交于点P（
| 3 |
| 5 |
| 4 |
| 5 |
| 5π |
| 12 |
考点：函数y=Asin（ωx+φ）的图象变换,任意角的三角函数的定义
专题：三角函数的求值
分析：（1）由函数的解析式结合且f（
）=
，求得A的值．
（2）由题意可知sinθ=
，cosθ=
，f(x)=3 sin(x+
)，利用三角恒等变换化简f（
-θ），可得结果．
| 5π |
| 12 |
3
| ||
| 2 |
（2）由题意可知sinθ=
| 4 |
| 5 |
| 3 |
| 5 |
| π |
| 3 |
| 5π |
| 12 |
解答：
解：（1）∵函数f（x）=Asin（x+
），f(
)=Asin(
+
)=Asin
=
，∴A=
•
=3．
（2）由题意可知sinθ=
，cosθ=
，且由（1）得：f(x)=3 sin(x+
)，
∴f(
-θ)=3sin(
-θ+
)=3sin(
-θ)=3sin
cosθ-3cos
sinθ=
．
| π |
| 3 |
| 5π |
| 12 |
| 5π |
| 12 |
| π |
| 3 |
| 3π |
| 4 |
3
| ||
| 2 |
3
| ||
| 2 |
| 2 |
（2）由题意可知sinθ=
| 4 |
| 5 |
| 3 |
| 5 |
| π |
| 3 |
∴f(
| 5π |
| 12 |
| 5π |
| 12 |
| π |
| 3 |
| 3π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
21
| ||
| 10 |
点评：本题主要考查任意角的三角函数的定义，三角函数的恒等变换及化简求值，属于基础题．
练习册系列答案
相关题目
已知直线a、b、c及平面α，它们具备下列哪组条件时，有b∥c成立（ ）
| A、b⊥a且c⊥a |
| B、b⊥α且c⊥α |
| C、b、c和α所成的角相等 |
| D、b∥α且c∥α |
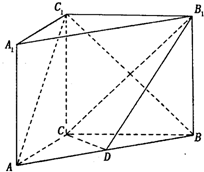如图，在直三棱柱ABC-A1B1C1中，AC=3，BC=4，AB=5，AA1=4，点D是AB的中点，
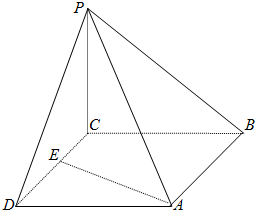如图，四棱锥P-ABCD的底面为正方形，平面PCD⊥平面ABCD，平面PBC⊥平面ABCD，E为线段CD上任意一点（不包括端点）．