题目内容
函数f(x)=
ax3+x2+x+1(a≠0)在区间(0,1]上单调递增,则实数a的取值范围为( )
| 1 |
| 3 |
| A、(-∞,-3] |
| B、[-3,0)∪(0,+∞) |
| C、(-∞,-3)∪(0,+∞) |
| D、[-3,0) |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:问题转化为a≥-
-
在区间(0,1]上恒成立,令g(x)=-
-
,(0<x≤1),求出函数g(x)的导数,得到其单调性,从而求出g(x)的最大值,进而求出a的范围.
| 2 |
| x |
| 1 |
| x2 |
| 2 |
| x |
| 1 |
| x2 |
解答:
解:∵f(x)=
ax3+x2+x+1(a≠0)在区间(0,1]上单调递增,
∴f′(x)=ax2+2x+1≥0在区间(0,1]上恒成立,
∴a≥-
-
在区间(0,1]上恒成立,
令g(x)=-
-
,(0<x≤1),
∴g′(x)=
+
>0,
∴g(x)在(0,1]单调递增,
∴g(x)max=g(1)=-3,
∴a≥-3,且a≠0,
故选:B.
| 1 |
| 3 |
∴f′(x)=ax2+2x+1≥0在区间(0,1]上恒成立,
∴a≥-
| 2 |
| x |
| 1 |
| x2 |
令g(x)=-
| 2 |
| x |
| 1 |
| x2 |
∴g′(x)=
| 2 |
| x2 |
| 2 |
| x3 |
∴g(x)在(0,1]单调递增,
∴g(x)max=g(1)=-3,
∴a≥-3,且a≠0,
故选:B.
点评:本题考查了函数的单调性,考查了导数的应用,考查了转化思想,是一道中档题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
函数f(x)=(x-5)0+(x-2)-
的定义域是( )
| 1 |
| 3 |
| A、{x|x∈R且x≠5,x≠2} |
| B、{x|x>2} |
| C、{x|x>5} |
| D、{x|2<x<5或x>5} |
双曲线
-
=1与椭圆
+
=1(a>0,m>b>0)的离心率互为倒数,则( )
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| m2 |
| y2 |
| b2 |
| A、a2+b2=m2 |
| B、a+b=m |
| C、a2=b2+m2 |
| D、a=b+m |
直线l的方向向量
=(-1,1,1),平面π的法向量为
=(2,x2+x,-x),若直线l∥平面π,则实数x的值为( )
| s |
| n |
| A、-2 | ||
B、-
| ||
C、
| ||
D、±
|
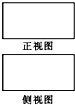 如图是长和宽分别相等的两个矩形,给定下列四个命题:
如图是长和宽分别相等的两个矩形,给定下列四个命题: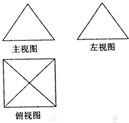 一个几何体的三视图如图所示,其中主(正)视图是边长为2的正三角形,俯视图是正方形,那么该几何体的左(侧)视图的面积是( )
一个几何体的三视图如图所示,其中主(正)视图是边长为2的正三角形,俯视图是正方形,那么该几何体的左(侧)视图的面积是( )