题目内容

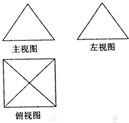一个几何体的三视图如图所示，其中主（正）视图是边长为2的正三角形，俯视图是正方形，那么该几何体的左（侧）视图的面积是（　　）
A、2
3
B、
3
C、4
D、2
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由题意可知左视图与主视图形状完全一样是正三角形，可得结论．
解答： 解：由题意可知左视图与主视图形状完全一样是正三角形，
因为主（正）视图是边长为2的正三角形，
所以几何体的左（侧）视图的面积S=
3
4
×22=
3

故选：B．
点评：本题考查由三视图求面积、体积，求解的关键是根据所给的三视图判断出几何体的几何特征．
练习册系列答案
相关题目
若命题“?x∈R，使x2+ax+1＜0”的否定是真命题，则实数a的取值范围是
 
．
过双曲线
y2
3
-x2=1上任一点P向两渐近线做垂线，垂足分别为A、B，则|AB|的最小值为
 
．
若函数f（x）关于点（a，0）和（b，0）对称（a≠b），则函数f（x）的一个周期T=
 
．
设双曲线C经过点（2，2），且与
y2
4
-x2=1具有相同渐进线，则双曲线C的方程为
 
．
函数f（x）=
1
3
ax3+x2+x+1（a≠0）在区间（0，1]上单调递增，则实数a的取值范围为（　　）
A、（-∞，-3]
B、[-3，0）∪（0，+∞）
C、（-∞，-3）∪（0，+∞）
D、[-3，0）
已知f（x）=|2x-
3
4
|+|2x+
5
4
|，设m，n∈R+，且m+n=1．
（Ⅰ）求不等式f（x）≤
5
2
的解集；
（Ⅱ）求证：
2m+1
+
2n+1
≤2
f(x)
．
已知
OA
=（x+
5
，y），
OB
=（x-
5
，y），且|
OA
|+|
OB
|=6，则|2x-3y-12|的最大值为
 
．
如图，直观图所表示的平面图形是（　　）
A、正三角形B、直角三角形
C、锐角三角形D、钝角三角形

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网