题目内容
已知函数f(x)=ex-ax-1(a∈R).
(1)求函数f(x)的单调区间;
(2)函数F(x)=f(x)-x1nx在定义域内是否存在零点?若存在,请指出有几个零点;若不存在,请说明理由:
(3)若g(x)=ln(ex-1)-lnx,当x∈(0,+∞)时,不等式f(g(x))<f(x)恒成立,求a的取值范围.
(1)求函数f(x)的单调区间;
(2)函数F(x)=f(x)-x1nx在定义域内是否存在零点?若存在,请指出有几个零点;若不存在,请说明理由:
(3)若g(x)=ln(ex-1)-lnx,当x∈(0,+∞)时,不等式f(g(x))<f(x)恒成立,求a的取值范围.
考点:利用导数研究函数的单调性,函数的定义域及其求法
专题:计算题,函数的性质及应用,导数的综合应用
分析:(1)求导f′(x)=ex-a;由导数的正负确定函数的单调性;
(2)先求函数F(x)=f(x)-x1nx的定义域,由F(x)=0可化为a=
-lnx,(x>0),从而令h(x)=
-lnx,(x>0),求导h′(x)=
,从而由导数求单调性并求最值;
(3)当x>0时,ex-1>x,故对?x>0,g(x)>0;构造函数H(x)=xex-ex+1(x>0),则H′(x)=xex>0;从而由导数确定恒成立问题.
(2)先求函数F(x)=f(x)-x1nx的定义域,由F(x)=0可化为a=
| ex-1 |
| x |
| ex-1 |
| x |
| (ex-1)(x-1) |
| x2 |
(3)当x>0时,ex-1>x,故对?x>0,g(x)>0;构造函数H(x)=xex-ex+1(x>0),则H′(x)=xex>0;从而由导数确定恒成立问题.
解答:
解:(1)∵f(x)=ex-ax-1,
∴f′(x)=ex-a;
当a≤0时,f′(x)>0;函数f(x)在R上是增函数;
当a>0时,当x>lna时,f′(x)>0,当x<lna时,f′(x)<0;
函数f(x)的单调增区间为(lna,+∞),单调减区间为(-∞,lna);
综上所述,当a≤0时,函数f(x)在R上是增函数;
当a>0时,函数f(x)的单调增区间为(lna,+∞),单调减区间为(-∞,lna);
(2)F(x)=f(x)-x1nx的定义域为(0,+∞),
由F(x)=0得,a=
-lnx,(x>0),
令h(x)=
-lnx,(x>0),则h′(x)=
,
由于x>0,ex-1>0;当x>1时,h′(x)>0;当0<x<1,h′(x)<0;
故函数h(x)在(0,1)上单调递减,在(1,+∞)上单调递增;
故h(x)≥h(1)=e-1;
又由(1)知,当a=1时,对?x>0,有f(x)>f(lna)=0;
即ex-1>x,故
>1;
∵x>0,∴
>0,
当x→0时,lnx→-∞,∴h(x)→+∞;
当a>e-1时,函数F(x)有两个不同的零点,
当a=e-1时,函数F(x)有且级有一个零点,
当a<e-1时,函数F(x)没有零点;
(3)由(2)知,当x>0时,ex-1>x,故对?x>0,g(x)>0;
构造函数H(x)=xex-ex+1(x>0),则H′(x)=xex>0;
故函数H(x)在(0,+∞)上单调递增,
则H(x)>H(0),
则?x>0,xex-ex+1>0成立,
当a≤1时,由(1)知,f(x)在(lna,+∞)上单调递增,在(0,lna)上单调递减,
帮当0<x<lna时,0<g(x)<x<lna,
所以f(g(x))>f(x),则不满足题意,
所以满足题意的a的取值范围是(-∞,1].
∴f′(x)=ex-a;
当a≤0时,f′(x)>0;函数f(x)在R上是增函数;
当a>0时,当x>lna时,f′(x)>0,当x<lna时,f′(x)<0;
函数f(x)的单调增区间为(lna,+∞),单调减区间为(-∞,lna);
综上所述,当a≤0时,函数f(x)在R上是增函数;
当a>0时,函数f(x)的单调增区间为(lna,+∞),单调减区间为(-∞,lna);
(2)F(x)=f(x)-x1nx的定义域为(0,+∞),
由F(x)=0得,a=
| ex-1 |
| x |
令h(x)=
| ex-1 |
| x |
| (ex-1)(x-1) |
| x2 |
由于x>0,ex-1>0;当x>1时,h′(x)>0;当0<x<1,h′(x)<0;
故函数h(x)在(0,1)上单调递减,在(1,+∞)上单调递增;
故h(x)≥h(1)=e-1;
又由(1)知,当a=1时,对?x>0,有f(x)>f(lna)=0;
即ex-1>x,故
| ex-1 |
| x |
∵x>0,∴
| ex-1 |
| x |
当x→0时,lnx→-∞,∴h(x)→+∞;
当a>e-1时,函数F(x)有两个不同的零点,
当a=e-1时,函数F(x)有且级有一个零点,
当a<e-1时,函数F(x)没有零点;
(3)由(2)知,当x>0时,ex-1>x,故对?x>0,g(x)>0;
构造函数H(x)=xex-ex+1(x>0),则H′(x)=xex>0;
故函数H(x)在(0,+∞)上单调递增,
则H(x)>H(0),
则?x>0,xex-ex+1>0成立,
当a≤1时,由(1)知,f(x)在(lna,+∞)上单调递增,在(0,lna)上单调递减,
帮当0<x<lna时,0<g(x)<x<lna,
所以f(g(x))>f(x),则不满足题意,
所以满足题意的a的取值范围是(-∞,1].
点评:本题考查了导数的综合应用及恒成立问题,属于中档题.

练习册系列答案
相关题目
函数f(x)=
ax3+x2+x+1(a≠0)在区间(0,1]上单调递增,则实数a的取值范围为( )
| 1 |
| 3 |
| A、(-∞,-3] |
| B、[-3,0)∪(0,+∞) |
| C、(-∞,-3)∪(0,+∞) |
| D、[-3,0) |
甲、乙两人向同一目标射击,命中率分别为0.4、0.5,则恰有一人命中的概率为( )
| A、0.9 | B、0.2 |
| C、0.7 | D、0.5 |
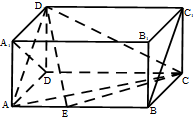 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动 某果林培育基地从其培育的一批幼苗中随机选取了100株,测量其高度(单位:厘米),并将这些数据绘制成频率分布直方图(如图).若要从高度在[120,130),[130,140),[140,150]三组内的幼苗中,用分层抽样的方法选取30株送给友好单位,则从高度在[140,150]内的幼苗中选取的株数应为( )
某果林培育基地从其培育的一批幼苗中随机选取了100株,测量其高度(单位:厘米),并将这些数据绘制成频率分布直方图(如图).若要从高度在[120,130),[130,140),[140,150]三组内的幼苗中,用分层抽样的方法选取30株送给友好单位,则从高度在[140,150]内的幼苗中选取的株数应为( )