题目内容
函数f(x)=(x-5)0+(x-2)-
的定义域是( )
| 1 |
| 3 |
| A、{x|x∈R且x≠5,x≠2} |
| B、{x|x>2} |
| C、{x|x>5} |
| D、{x|2<x<5或x>5} |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据指数幂的性质得到不等式组,解出即可.
解答:
解:由题意得:
,解得:x≠5,且x≠2,
故选:A.
|
故选:A.
点评:本题考查了函数的定义域问题,考查了指数幂的性质,是一道基础题.

练习册系列答案
相关题目
有下列四个命题
①“若x+y=0,则x,y互为相反数”的否命题
②“若q>1则x2+2x+q=0有实根“的逆否命题
③”tanα=tanβ,则α=β”的逆命题
④若x≠2且y≠1,则x+y≠3
其中真命题为( )
①“若x+y=0,则x,y互为相反数”的否命题
②“若q>1则x2+2x+q=0有实根“的逆否命题
③”tanα=tanβ,则α=β”的逆命题
④若x≠2且y≠1,则x+y≠3
其中真命题为( )
| A、①② | B、①③ | C、①④ | D、① |
函数f(x)=
ax3+x2+x+1(a≠0)在区间(0,1]上单调递增,则实数a的取值范围为( )
| 1 |
| 3 |
| A、(-∞,-3] |
| B、[-3,0)∪(0,+∞) |
| C、(-∞,-3)∪(0,+∞) |
| D、[-3,0) |
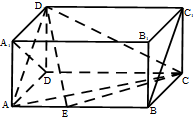 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动