题目内容
18.圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的位置关系为( )| A. | 内切 | B. | 外切 | C. | 相交 | D. | 外离 |
分析 由两圆的方程可得圆心坐标及其半径,判断圆心距与两圆的半径和差的关系即可得出.
解答 解:圆C(x+2)2+y2=4的圆心C(-2,0),半径r=2;
圆M(x-2)2+(y-1)2=9的圆心M(2,1),半径 R=3.
∴|CM|=$\sqrt{(-2-2)^{2}+1}$=$\sqrt{17}$,R-r=3-2=1,R+r=3+2=5.
∴R-r<$\sqrt{17}$<R+r.
∴两圆相交.
故选:C.
点评 本题考查了判断两圆的位置关系的方法,属于基础题.

练习册系列答案
相关题目
8.某三棱锥的三视图如图所示,则俯视图的面积为( )


| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |
9.已知一组样本数据(xi,yi)如表
设其线性回归方程$\widehat{y}$=bx+a,若已求出b=0.7,则线性回归方程为( )
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| A. | $\widehat{y}$=0.7x+0.35 | B. | $\widehat{y}$=0.7x+4.5 | C. | $\widehat{y}$=0.7x-0.35 | D. | $\widehat{y}$=0.7x-4.5 |
13.若实数x,y满足$\left\{\begin{array}{l}x-y+1≥0\\ x+y≥0\\ x≤0\end{array}\right.$,则z=x-2y的最小值是( )
| A. | 0 | B. | $\frac{3}{2}$ | C. | -2 | D. | $-\frac{3}{2}$ |
3.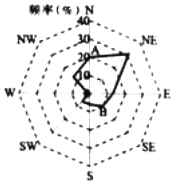 如图所示为某城市去年风向频率图,图中A点表示该城市去年有的天数吹北风,点表示该城B市去年有10%的天数吹东南风,下面叙述不正确的是( )
如图所示为某城市去年风向频率图,图中A点表示该城市去年有的天数吹北风,点表示该城B市去年有10%的天数吹东南风,下面叙述不正确的是( )
 如图所示为某城市去年风向频率图,图中A点表示该城市去年有的天数吹北风,点表示该城B市去年有10%的天数吹东南风,下面叙述不正确的是( )
如图所示为某城市去年风向频率图,图中A点表示该城市去年有的天数吹北风,点表示该城B市去年有10%的天数吹东南风,下面叙述不正确的是( )| A. | 去年吹西北风和吹东风的频率接近 | B. | 去年几乎不吹西风 | ||
| C. | 去年吹东风的天数超过100天 | D. | 去年吹西南风的频率为15%左右 |
7.若sinαsinβ=1,则cos(α+β)=( )
| A. | 1 | B. | -1 | C. | 0 | D. | 0或-1 |
8.在△ABC中,角A、B、C的对边分别为a,b,c,且b(2sinB+sinA)+(2a+b)sinA=2csinC,则C=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
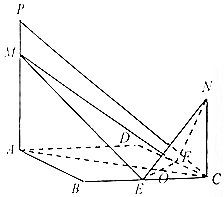 如图,已知E,F分别是正方形ABCD边BC、CD的中点,EF与AC交于点O,PA,NC都垂直于平面ABCD,且PA=AB=4,NC=2,M是线段PA上的一动点.
如图,已知E,F分别是正方形ABCD边BC、CD的中点,EF与AC交于点O,PA,NC都垂直于平面ABCD,且PA=AB=4,NC=2,M是线段PA上的一动点.