题目内容
10.三位女同学两位男同学站成一排,男同学不站两端的排法总数为36.(用数字寺写答案)分析 根据题意,假设5个人分别对应5个空位,男同学不站两端,有3个位置可选;而其他3人对应其他3个位置,对其全排列,可得其排法数目,由分步计数原理计算可得答案.
解答 解:假设5个人分别对应5个空位,男同学不站在两端,有3个位置可选;
则其他3人对应其他3个位置,有A33=6种情况,
则不同排列方法种数6×6=36种.
故答案为36.
点评 本题考查排列、组合的运用,一般要先处理特殊(受到限制的)元素.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.若直线l:(a2-1)x-y-2a+1=0不过第二象限,则a的取值范围为( )
| A. | (-∞,$\frac{1}{2}$] | B. | [$\frac{1}{2}$,+∞) | C. | (-∞,1] | D. | [1,+∞) |
18.圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的位置关系为( )
| A. | 内切 | B. | 外切 | C. | 相交 | D. | 外离 |
5.已知复数z=$\frac{2i}{1-i}$,其中i 为虚数单位,则z所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.已知函数$f(x)=|x-a|,g(x)=\frac{2}{x}+1$,若两函数的图象有且只有三个不同的公共点,则实数a的取值范围是( )
| A. | (-∞,-2) | B. | $(1+2\sqrt{2},+∞)$ | C. | $(-∞,-2]∪[1+2\sqrt{2},+∞)$ | D. | $(-∞,-2)∪(1+2\sqrt{2},+∞)$ |
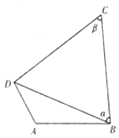 如图,在圆内接四边形ABCD中,AB=2,AD=1,$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ
如图,在圆内接四边形ABCD中,AB=2,AD=1,$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ