题目内容
13．某变速运动的物体，路程s（米）随时间t（秒）变化的函数关系式是s=t2-2t+5，则此物体在t=1秒时的瞬时速度为（ ）| A． | 2m/s | B． | 0m/s | C． | 4m/s | D． | -4m/s |
分析 根据导数物理意义求函数的导数即可．
解答 解：∵路程s（米）随时间t（秒）变化的函数关系式是s=t2-2t+5，
∴函数的导数s′（t）=2t-2，
则此物体在t=1秒时的瞬时速度为s′（1）=2-2=0，
故选：B．
点评 本题主要考查导数的计算，根据导数的物理意义求函数的导数是解决本题的关键．
练习册系列答案
相关题目
3．
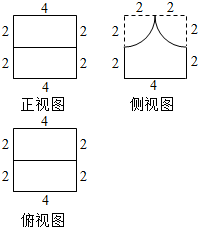某几何体的三视图如图所示（其中侧视图为正方形上半部分在两个角上各截去四分之一圆），则该几何体的表面积为（ ）
某几何体的三视图如图所示（其中侧视图为正方形上半部分在两个角上各截去四分之一圆），则该几何体的表面积为（ ）| A． | 48+4π | B． | 48+8π | C． | 64+4π | D． | 64+8π |
1．下列命题正确的是（ ）
| A． | “b2=ac”是“a，b，c成等比数列”的充要条件 | |
| B． | “?x∈R，x2＞0”的否定是“?x0∈R，x02＞0” | |
| C． | “若a=-4，则函数f（x）=ax2+4x-1只有唯一一个零点”的逆命题为真命题 | |
| D． | “函数f（x）=lnx2与函数g（x）=$\left\{\begin{array}{l}{2lnx，x＞0}\\{2ln（-x），x＜0}\end{array}\right.$的图象相同” |
8．已知函数y=f（x-1）是奇函数，且f（2）=1，则f（-4）=（ ）
| A． | 1 | B． | 3 | C． | -1 | D． | -3 |
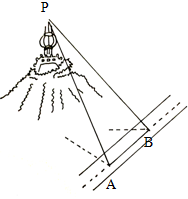沿着山边一条平直的公路测量山顶一建筑物的高度，如图所示，已知A处测量建筑物顶部的仰角为60°，B处测量建筑物顶部的仰角为30°，已知图中
3．图中阴影部分所表示的集合是（ ）
| A． | （A∪B）∪（B∪C） | B． | [∁U（A∩C）]∪B | C． | （A∪C）∩（∁UB） | D． | B∩[∁U（A∪C）] |