题目内容
10.(1)实数a,b满足不等式组$\left\{\begin{array}{l}{b>0}\\{a+b+1<0}\\{3a+b+9>0}\end{array}\right.$,则在坐标平面aOb内,点(a,b)对应的区域S,求目标函数z=2a-b的取值范围.(2)过点(-5,1)的光线经x轴反射后的光线过区域S,求反射光线所在直线l经过区域S内的整点(即横纵坐标为整数的点)时直线l的方程.
分析 (1)由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案;
(2)求出可行域内的整点坐标,结合过点(-5,1)的光线经x轴反射后的光线必过点(-5,-1),再由直线上的两点求得直线l的方程.
解答  解:(1)由约束条件$\left\{\begin{array}{l}{b>0}\\{a+b+1<0}\\{3a+b+9>0}\end{array}\right.$作出可行域如图阴影部分所示,
解:(1)由约束条件$\left\{\begin{array}{l}{b>0}\\{a+b+1<0}\\{3a+b+9>0}\end{array}\right.$作出可行域如图阴影部分所示,
联立方程组求得图中A,B,C三点的坐标分别为(-4,3),(-3,0),(-1,0),
令z=2a-b,则直线b=2a-z经过点A时z取得最小值,经过点C时z取得最大值,即zmin=-11,zmax=-2,
又A,B,C三点的值没有取到,∴-11<z<-2;
(2)过点(-5,1)的光线经x轴反射后的光线必过点(-5,-1),由图可知可能满足条件的整点为
(-3,1),(-3,2),(-2,2),(-2,1),再结合不等式知点(-3,1)符合条件,
∴此时直线方程为:$y+1=\frac{1-(-1)}{-3-(-5)}(x+5)$,即y=x+4.
点评 本题考查简单的线性规划,考查了数形结合的数学思想方法和数学转化思想方法,是中档题.

练习册系列答案
相关题目
1.下列命题正确的是( )
| A. | “b2=ac”是“a,b,c成等比数列”的充要条件 | |
| B. | “?x∈R,x2>0”的否定是“?x0∈R,x02>0” | |
| C. | “若a=-4,则函数f(x)=ax2+4x-1只有唯一一个零点”的逆命题为真命题 | |
| D. | “函数f(x)=lnx2与函数g(x)=$\left\{\begin{array}{l}{2lnx,x>0}\\{2ln(-x),x<0}\end{array}\right.$的图象相同” |
15.已知Sn为等差数列{an}的前n项和,若a5=7,则S9=( )
| A. | 45 | B. | 53 | C. | 63 | D. | 72 |
19.函数$f(x)={log_3}x-{(\frac{1}{2})^x}$,若实数x0是函数f(x)的零点,且0<x1<x0,则f(x1)的值为( )
| A. | 恒为正 | B. | 等于零 | C. | 恒为负 | D. | 不小于零 |
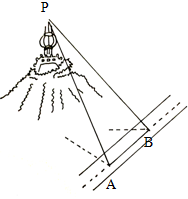 沿着山边一条平直的公路测量山顶一建筑物的高度,如图所示,已知A处测量建筑物顶部的仰角为60°,B处测量建筑物顶部的仰角为30°,已知图中
沿着山边一条平直的公路测量山顶一建筑物的高度,如图所示,已知A处测量建筑物顶部的仰角为60°,B处测量建筑物顶部的仰角为30°,已知图中