题目内容
7.设{an}是一个公差不为零的等差数列,其前n项和为Sn,已知S9=90,且a1,a2,a4成等比数列.(1)求数列{an}的通项公式;
(2)设bn=$\frac{1}{{{a_n}{a_{n+1}}}}$,求数列{bn}的前n项和Tn.
分析 (1)设等差数列{an}的公差为d(d≠0),由a1,a2,a4成等比数列,可得$a_2^2={a_1}{a_4}$,即${({a_1}+d)^2}={a_1}({a_1}+3d)$,由${S_9}=9{a_1}+\frac{9×8}{2}d=90$,联立解出即可得出.
(2)利用“裂项求和”即可得出.
解答 解:(1)设等差数列{an}的公差为d(d≠0),则a2=a1+d,a4=a1+3d,
由a1,a2,a4成等比数列,可得$a_2^2={a_1}{a_4}$,
即${({a_1}+d)^2}={a_1}({a_1}+3d)$,
整理,可得a1=d.
由${S_9}=9{a_1}+\frac{9×8}{2}d=90$,可得a1=d=2,
∴an=a1+(n-1)d=2n.
(2)由于an=2n,
所以${b_n}=\frac{1}{4n(n+1)}=\frac{1}{4}(\frac{1}{n}-\frac{1}{n+1})$,
从而${T_n}=\frac{1}{4}[(\frac{1}{1}-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{4})+…+(\frac{1}{n}-\frac{1}{n+1})]=\frac{1}{4}×\frac{n}{n+1}=\frac{n}{4n+4}$,
即数列{bn}的前n项和为${T_n}=\frac{n}{4n+4}$.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
17.某中学高一、高二各有一个文科和一个理科两个实验班,现将这四个班级随机分配到上海交通大学和浙江大学两所高校进行研学,每个班级去一所高校,每所高校至少有一个班级去,则恰好有一个文科班和一个理科班分配到上海交通大学的概率为( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
15.已知Sn为等差数列{an}的前n项和,若a5=7,则S9=( )
| A. | 45 | B. | 53 | C. | 63 | D. | 72 |
19.函数$f(x)={log_3}x-{(\frac{1}{2})^x}$,若实数x0是函数f(x)的零点,且0<x1<x0,则f(x1)的值为( )
| A. | 恒为正 | B. | 等于零 | C. | 恒为负 | D. | 不小于零 |
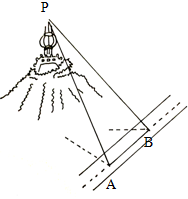 沿着山边一条平直的公路测量山顶一建筑物的高度,如图所示,已知A处测量建筑物顶部的仰角为60°,B处测量建筑物顶部的仰角为30°,已知图中
沿着山边一条平直的公路测量山顶一建筑物的高度,如图所示,已知A处测量建筑物顶部的仰角为60°,B处测量建筑物顶部的仰角为30°,已知图中