题目内容
8．函数f（x）=lnx+2x的图象在点（1，2）处的切线方程为3x-y-1=0．分析 求出函数的导数，求得切线的斜率，由直线的点斜式方程可得所求切线的方程．
解答 解：函数f（x）=lnx+2x的导数为f′（x）=$\frac{1}{x}$+2，
在点（1，2）处的切线斜率为k=3，
则在点（1，2）处的切线方程为y-2=3（x-1），
即为3x-y-1=0．
故答案为：3x-y-1=0．
点评 本题考查导数的运用：求切线的方程，正确求导和运用直线的点斜式方程是解题的关键．
练习册系列答案
相关题目
18．一个椭圆的半焦距为2，离心率e=$\frac{2}{3}$，则它的短轴长是（ ）
| A． | 3 | B． | $\sqrt{5}$ | C． | 2$\sqrt{5}$ | D． | 6 |
3．
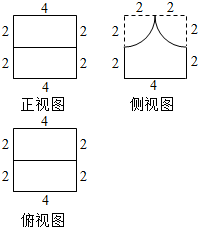某几何体的三视图如图所示（其中侧视图为正方形上半部分在两个角上各截去四分之一圆），则该几何体的表面积为（ ）
某几何体的三视图如图所示（其中侧视图为正方形上半部分在两个角上各截去四分之一圆），则该几何体的表面积为（ ）| A． | 48+4π | B． | 48+8π | C． | 64+4π | D． | 64+8π |
17．某中学高一、高二各有一个文科和一个理科两个实验班，现将这四个班级随机分配到上海交通大学和浙江大学两所高校进行研学，每个班级去一所高校，每所高校至少有一个班级去，则恰好有一个文科班和一个理科班分配到上海交通大学的概率为（ ）
| A． | $\frac{1}{7}$ | B． | $\frac{2}{7}$ | C． | $\frac{3}{7}$ | D． | $\frac{4}{7}$ |
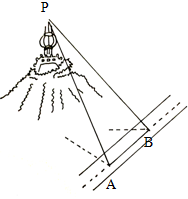沿着山边一条平直的公路测量山顶一建筑物的高度，如图所示，已知A处测量建筑物顶部的仰角为60°，B处测量建筑物顶部的仰角为30°，已知图中