题目内容
6.设函数f(x)=x2+alnx+1(x>0).(1)若f(3)=5,求f($\frac{1}{3}$)的值;
(2)若x>0时,f(x)≥1成立,求a的取值范围.
分析 (1)由f(3)=5得出aln3=-5,再求出f($\frac{1}{3}$)的值.
(2)alnx≥-x2.然后讨论lnx的符号分离参数,转化为求-$\frac{{x}^{2}}{lnx}$得最大值或最小值问题.
解答 解:(1)∵f(3)=10+aln3=5,∴aln3=-5.∴f($\frac{1}{3}$)=$\frac{10}{9}$+aln$\frac{1}{3}$=$\frac{10}{9}$-aln3=$\frac{10}{9}+5$=$\frac{55}{9}$.
(2)∵x2+alnx+1≥1,∴alnx≥-x2.
①若lnx=0,即x=1时,显然上式恒成立.
②若lnx>0,即x>1时,a≥-$\frac{{x}^{2}}{lnx}$.令g(x)=-$\frac{{x}^{2}}{lnx}$.则g′(x)=$\frac{x(1-2lnx)}{l{n}^{2}x}$,
∴当1<x$<\sqrt{e}$时,g′(x)>0,当x$>\sqrt{e}$时,g′(x)<0,
∴当x=$\sqrt{e}$时,g(x)取得最大值g($\sqrt{e}$)=-2e.∴a≥-2e.
③若lnx<0,即0<x<1时,a≤-$\frac{{x}^{2}}{lnx}$,由②讨论可知g(x)在(0,1)上是增函数,且g(x)>0,∴a≤0.
综上,a的取值范围是[-2e,0].
点评 本题考查了函数求值及函数恒成立问题,分离参数法是常用解题方法之一.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
17.某中学高一、高二各有一个文科和一个理科两个实验班,现将这四个班级随机分配到上海交通大学和浙江大学两所高校进行研学,每个班级去一所高校,每所高校至少有一个班级去,则恰好有一个文科班和一个理科班分配到上海交通大学的概率为( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
1.下列命题正确的是( )
| A. | “b2=ac”是“a,b,c成等比数列”的充要条件 | |
| B. | “?x∈R,x2>0”的否定是“?x0∈R,x02>0” | |
| C. | “若a=-4,则函数f(x)=ax2+4x-1只有唯一一个零点”的逆命题为真命题 | |
| D. | “函数f(x)=lnx2与函数g(x)=$\left\{\begin{array}{l}{2lnx,x>0}\\{2ln(-x),x<0}\end{array}\right.$的图象相同” |
15.已知Sn为等差数列{an}的前n项和,若a5=7,则S9=( )
| A. | 45 | B. | 53 | C. | 63 | D. | 72 |
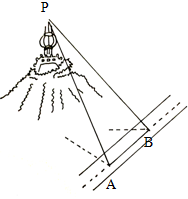 沿着山边一条平直的公路测量山顶一建筑物的高度,如图所示,已知A处测量建筑物顶部的仰角为60°,B处测量建筑物顶部的仰角为30°,已知图中
沿着山边一条平直的公路测量山顶一建筑物的高度,如图所示,已知A处测量建筑物顶部的仰角为60°,B处测量建筑物顶部的仰角为30°,已知图中