题目内容
已知命题p:?x∈R,使sinx=
;命题q:?x∈R,都有x2+x+1>0.给出下列结论:
①命题“p∧q”是真命题;
②命题“¬p∨q”是假命题
③命题“¬p∨q”是真命题;
④命题“p∨¬q”是假命题;
其中正确的是( )
| ||
| 2 |
①命题“p∧q”是真命题;
②命题“¬p∨q”是假命题
③命题“¬p∨q”是真命题;
④命题“p∨¬q”是假命题;
其中正确的是( )
| A、②③ | B、②④ | C、③④ | D、①②③ |
考点:命题的真假判断与应用
专题:简易逻辑
分析:考察命题真假判断,涉及三角函数值的范围和二次不等式.
解答:
解:∵
>1,结合正弦函数的性质,易得命题p为假命题,
又∵x2+x+1=(x+
)2+
>0恒成立,∴q为真命题,
故¬p是真命题,¬q是假命题;
所以①p∧q是假命题,①错误;
p∧¬q是假命题,②正确,③错误;
命题“p∨¬q”是假命题,④正确;
故答案为:②④
故选:B.
| ||
| 2 |
又∵x2+x+1=(x+
| 1 |
| 2 |
| 3 |
| 4 |
故¬p是真命题,¬q是假命题;
所以①p∧q是假命题,①错误;
p∧¬q是假命题,②正确,③错误;
命题“p∨¬q”是假命题,④正确;
故答案为:②④
故选:B.
点评:要注意或∨全假时假、且∧全假时假、非¬真假相反.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数f(x)=
+
(0<x<
)的最小值为( )
| 2 |
| x |
| 9 |
| 1-2x |
| 1 |
| 2 |
| A、169 | B、121 |
| C、25 | D、16 |
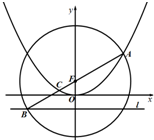 如图,已知点F是抛物线x2=4y的焦点,直线l为准线,点A是抛物线上一点.以F点为圆心,|AF|为半径作圆M交抛物线的准线l于点B.若A,B,F三点共线,则|AC|=( )
如图,已知点F是抛物线x2=4y的焦点,直线l为准线,点A是抛物线上一点.以F点为圆心,|AF|为半径作圆M交抛物线的准线l于点B.若A,B,F三点共线,则|AC|=( )