题目内容
已知数列{an}是一个等差数列且S9=-18,S11=22,
(1)求{an}通项公式;
(2)求{an}的前n项和Sn的最小值.
(1)求{an}通项公式;
(2)求{an}的前n项和Sn的最小值.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)根据等差数列的前n项和公式,建立方程组求出首项和公差,即可求{an}通项公式;
(2)求出数列的前n项和,利用二次函数的性质即可求出最值.
(2)求出数列的前n项和,利用二次函数的性质即可求出最值.
解答:
解:(1)设{an}的公差为d,则
,
∴a1=-18,d=4,
∴an=a1+(n-1)d=4n-22.
(2)法一:Sn=
=
=2n2-20n=2(n-5)2-50,
∴n=5时,Sn取得最小值-50. …(9分).
法二:由an=4n-22<0,得n<
,
∴当n=5时,Sn取得最小值S5=-18×5+
×4=-50.
|
∴a1=-18,d=4,
∴an=a1+(n-1)d=4n-22.
(2)法一:Sn=
| n(a1+an) |
| 2 |
| n(-18+4n-22) |
| 2 |
∴n=5时,Sn取得最小值-50. …(9分).
法二:由an=4n-22<0,得n<
| 22 |
| 4 |
∴当n=5时,Sn取得最小值S5=-18×5+
| 5×4 |
| 2 |
点评:本题主要考查等差数列的通项公式和前n项和公式的应用,要求熟练掌握相应的公式.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案
相关题目
已知复数z=(x2-2x-3)+(x-3)i(x∈R,i为虚数单位)为纯虚数,则x的值为( )
| A、-1或3 | B、0 | C、3 | D、-1 |
设集合A={x|x2-3x=0,x∈R},B={x|x2+3x=0,x∈R},则A∩B=( )
| A、{0} |
| B、{0,-3} |
| C、{0,3} |
| D、{0,-3,3} |
 如图四边形ABEF是等腰梯形,AB∥EF,AF=BE=2,EF=4
如图四边形ABEF是等腰梯形,AB∥EF,AF=BE=2,EF=4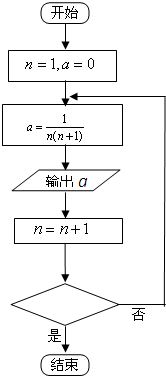 执行如图程序框图:
执行如图程序框图: