题目内容
设数列{an}的前n项和为Sn,已知2Sn+1=Sn+λ(n∈N*,λ为常数),a1=2,a2=1.
(1)求数列{an}的通项公式;
(2)求所有满足等式
=
成立的正整数m,n.
(1)求数列{an}的通项公式;
(2)求所有满足等式
| Sn-m |
| Sn+1-m |
| 1 |
| am+1 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)利用条件a1=2,a2=1建立方程组,即可求数列{an}的通项公式;
(2)求出Sn,利用等式
=
成立,解方程即可得到结论.
(2)求出Sn,利用等式
| Sn-m |
| Sn+1-m |
| 1 |
| am+1 |
解答:
解:(1)由题意,得2S2=S1+λ,求得λ=4.
所以,2Sn+1=Sn+4①
当n≥2时,2Sn=Sn-1+4②
①-②,得an+1=
an(n≥2),又a2=
a1,
所以数列{an}是首项为2,公比为
的等比数列.
所以{an}的通项公式为an=(
)n-2(n∈N*).
(2)由(1),得Sn=4(1-
),
由
=
,得1+
=1+am,化简得
=
,
即(4-m)2n-4=2m-1,即(4-m)2n=4+2m-1.(*)
因为2m-1+4>0,所以(4-m)•2n>0,所以m<4,
因为m∈N*,所以m=1或2或3.
当m=1时,由(*)得3×2n=5,所以无正整数解;
当m=2时,由(*)得2×2n=6,所以无正整数解;
当m=3时,由(*)得2n=8,所以n=3.
综上可知,存在符合条件的正整数m=n=3.
所以,2Sn+1=Sn+4①
当n≥2时,2Sn=Sn-1+4②
①-②,得an+1=
| 1 |
| 2 |
| 1 |
| 2 |
所以数列{an}是首项为2,公比为
| 1 |
| 2 |
所以{an}的通项公式为an=(
| 1 |
| 2 |
(2)由(1),得Sn=4(1-
| 1 |
| 2n |
由
| Sn-m |
| Sn+1-m |
| 1 |
| am+1 |
| an+1 |
| Sn-m |
| 2 |
| (4-m)2n-4 |
| 4 |
| 2m |
即(4-m)2n-4=2m-1,即(4-m)2n=4+2m-1.(*)
因为2m-1+4>0,所以(4-m)•2n>0,所以m<4,
因为m∈N*,所以m=1或2或3.
当m=1时,由(*)得3×2n=5,所以无正整数解;
当m=2时,由(*)得2×2n=6,所以无正整数解;
当m=3时,由(*)得2n=8,所以n=3.
综上可知,存在符合条件的正整数m=n=3.
点评:本题主要考查数列通项公式的求解,考查学生的计算能力.

练习册系列答案
相关题目
同时掷两颗骰子,得到点数和为8的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
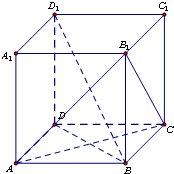 已知正方体ABCD-A1B1C1D1中,求证:
已知正方体ABCD-A1B1C1D1中,求证: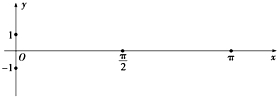 某简谐运动的图象对应的函数解析式为:y=
某简谐运动的图象对应的函数解析式为:y=