题目内容
设正数列{an}的前{an}项和为n,且2
=an+1.
(1)求数列{an}的首项a1;
(2)求数列{an}的通项公式;
(3)设bn=
,Tn是数列{bn}的前{an}项和,求使得Tn<
对所有n∈N*都成立的最小正整数m.
| Sn |
(1)求数列{an}的首项a1;
(2)求数列{an}的通项公式;
(3)设bn=
| 1 |
| anan+1 |
| m |
| 18 |
考点:数列与不等式的综合,数列递推式
专题:等差数列与等比数列
分析:(1)直接在递推式中取n=1求得a1;
(2)在递推式中取n=n+1得另一递推式,作差后得到数列{an}是等差数列并求得公差,代入等差数列的通项公式得答案;
(3)利用裂项相消法求出数列{bn}的前n项和,放缩后得到Tn<
,由
≤
求得使Tn<
对所有n∈N*都成立的最小正整数m.
(2)在递推式中取n=n+1得另一递推式,作差后得到数列{an}是等差数列并求得公差,代入等差数列的通项公式得答案;
(3)利用裂项相消法求出数列{bn}的前n项和,放缩后得到Tn<
| 1 |
| 2 |
| 1 |
| 2 |
| m |
| 18 |
| m |
| 18 |
解答:
解:(1)当n=1时,由2
=a1+1且S1=a1,解得a1=1;
(2)由2
=an+1,得4Sn=(an+1)2…①
∴4Sn+1=(an+1+1)2…②
②-①得:4Sn+1-4Sn=(an+1+1)2-(an+1)2,
化简,得(an+1+an)•(an+1-an-2)=0,
又由an>0,得an+1+an>0,
∴an+1-an-2=0,即an+1-an=2.
∴数列{an}是以1为首项,公差为2的等差数列,
∴an=a1+(n-1)×2,
即an=2n-1;
(3)把an=2n-1代入bn=
,得:
bn=
=
=
(
-
),
∴Tn=b1+b2+…bn=
[(1-
)+(
-
)+…+(
-
)]=
(1-
)<
.
∴要使Tn<
对所有n∈N*都成立,只需
≤
,即m≥9.
∴满足条件的最小正整数m=9.
| S1 |
(2)由2
| Sn |
∴4Sn+1=(an+1+1)2…②
②-①得:4Sn+1-4Sn=(an+1+1)2-(an+1)2,
化简,得(an+1+an)•(an+1-an-2)=0,
又由an>0,得an+1+an>0,
∴an+1-an-2=0,即an+1-an=2.
∴数列{an}是以1为首项,公差为2的等差数列,
∴an=a1+(n-1)×2,
即an=2n-1;
(3)把an=2n-1代入bn=
| 1 |
| anan+1 |
bn=
| 1 |
| anan+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=b1+b2+…bn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
∴要使Tn<
| m |
| 18 |
| 1 |
| 2 |
| m |
| 18 |
∴满足条件的最小正整数m=9.
点评:本题考查了数列递推式,考查了等差关系的确定,训练了裂项相消法求数列的和,考查了利用放缩法证明不等式,是中高档题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
等比数列{an}中,a2a4=16,则a1a5=( )
| A、4 | B、16 | C、-4 | D、-16 |
根据图所示程序框图,当输入10时,输出的是( )


| A、14.1 | B、19 |
| C、12 | D、-30 |
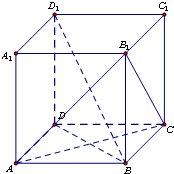 已知正方体ABCD-A1B1C1D1中,求证:
已知正方体ABCD-A1B1C1D1中,求证: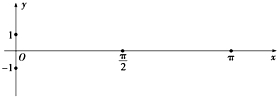 某简谐运动的图象对应的函数解析式为:y=
某简谐运动的图象对应的函数解析式为:y=