题目内容
已知命题P:实数a满足|a-1|<6,命题Q:集合A={x|x2+(a+2)x+1=0,x∈R},B={x|x≥0}且A∩B=∅.
(1)求命题Q为真命题时的实数a的取值范围;
(2)设P,Q皆为真时a的取值范围为集合S,T={y|y=x+
,x∈R,m>0},若∁RT⊆S,求m取值范围.
(1)求命题Q为真命题时的实数a的取值范围;
(2)设P,Q皆为真时a的取值范围为集合S,T={y|y=x+
| m |
| x |
考点:补集及其运算
专题:计算题,不等式的解法及应用,集合
分析:(1)若命题Q为真命题,则设x2+(a+2)x+1=0判别式为△,当△<0时,A=∅,此时△<0,当△≥0时,由A∩B=∅得
,解得,再求并集即可;
(2)求得P,Q皆为真时a的取值范围为集合S=(-4,7),再化简集合T,注意运用基本不等式,再求补集,最后根据集合的包含关系,列出不等式,解出即可.
|
(2)求得P,Q皆为真时a的取值范围为集合S=(-4,7),再化简集合T,注意运用基本不等式,再求补集,最后根据集合的包含关系,列出不等式,解出即可.
解答:
解:(1)若命题Q为真命题,则设x2+(a+2)x+1=0判别式为△,
当△<0时,A=∅,此时△=(a+2)2-4<0,-4<a<0;
当△≥0时,由A∩B=∅得
,即有
,解得a≥0.
综上可得,a>-4;
(2)若命题P为真,则|a-1|<6,解得-5<a<7.
则有P,Q皆为真时a的取值范围为集合S=(-4,7),
由于T={y|y=x+
,x∈R,m>0}={y|y≥2
或y≤-2
},
则∁RT={y|-2
<y<2
},
由于∁RT⊆S,则有2
≤7且-2
≥-4,即有0<m≤
且0<m≤4,
解得0<m≤4.
故m的取值范围是(0,4].
当△<0时,A=∅,此时△=(a+2)2-4<0,-4<a<0;
当△≥0时,由A∩B=∅得
|
|
综上可得,a>-4;
(2)若命题P为真,则|a-1|<6,解得-5<a<7.
则有P,Q皆为真时a的取值范围为集合S=(-4,7),
由于T={y|y=x+
| m |
| x |
| m |
| m |
则∁RT={y|-2
| m |
| m |
由于∁RT⊆S,则有2
| m |
| m |
| 49 |
| 4 |
解得0<m≤4.
故m的取值范围是(0,4].
点评:本题考查二次方程根的分布,注意运用二次函数的性质,考查集合的包含关系,以及集合的化简和基本不等式的运用,属于中档题和易错题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
用小立方块搭一个几何体,使它的正视图和俯视图如图所示,则它需要的小立方块的个数最多是( )
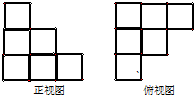

| A、12 | B、13 | C、14 | D、15 |
10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有( )
| A、a>b>c |
| B、b>c>a |
| C、c>a>b |
| D、c>b>a |