题目内容
已知x,y,z∈Z,且满足x+y+z=3,x3+y3+z3=3,求x2+y2+z2所有可能的值组成的集合.
考点:二维形式的柯西不等式
专题:综合题,不等式的解法及应用
分析:设x2+y2+z2=t,则xy+yz+xz=
,利用x3+y3+z3-3xyz=(x+y+z)(x2+y2+z2-xy-yz-zx),可得xyz=
,即可得出结论.
| 9-t |
| 2 |
| 11-3t |
| 2 |
解答:
解:设x2+y2+z2=t,则
∵(x+y+z)2=x2+y2+z2+2(xy+yz+xz),
即9=t+2(xy+yz+xz),
∴xy+yz+xz=
,
∵x3+y3+z3-3xyz=(x+y+z)(x2+y2+z2-xy-yz-zx),
∴3-3xyz=3(t-
),
∴xyz=
,
∵x,y,z∈Z,t>0,
∴t=1,3,
∴x2+y2+z2所有可能的值组成的集合为{1,3}.
∵(x+y+z)2=x2+y2+z2+2(xy+yz+xz),
即9=t+2(xy+yz+xz),
∴xy+yz+xz=
| 9-t |
| 2 |
∵x3+y3+z3-3xyz=(x+y+z)(x2+y2+z2-xy-yz-zx),
∴3-3xyz=3(t-
| 9-t |
| 2 |
∴xyz=
| 11-3t |
| 2 |
∵x,y,z∈Z,t>0,
∴t=1,3,
∴x2+y2+z2所有可能的值组成的集合为{1,3}.
点评:本题主要考查立方公式的知识点,解答本题的关键是求出xyz=
.
| 11-3t |
| 2 |

练习册系列答案
相关题目
化简
+
+
-
=( )
| AB |
| BD |
| CA |
| CD |
A、
| ||
B、
| ||
C、
| ||
D、
|
以下棱柱中,最多只有一对面互相平行的是( )
| A、三棱柱 | B、四棱柱 |
| C、八棱柱 | D、六棱柱 |
不等式|2x-1|≤3的解集为( )
| A、{x|-1≤x≤2} |
| B、{x|x≥2或x≤-1} |
| C、{x|-2≤x≤1} |
| D、{x|x≥1或x≤-2} |
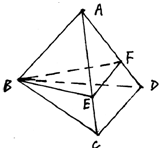 已知正三棱锥A-BCD中,底面边长为a,侧棱长为2a,过B点作与则棱AC、AD相交的截面BEF,在这个截面三角形中,求:
已知正三棱锥A-BCD中,底面边长为a,侧棱长为2a,过B点作与则棱AC、AD相交的截面BEF,在这个截面三角形中,求: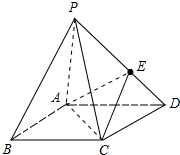 如图,底面是平行四边形的四棱锥P-ABCD,点E在PD上,且PE:ED=2:1,问:在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
如图,底面是平行四边形的四棱锥P-ABCD,点E在PD上,且PE:ED=2:1,问:在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.