题目内容
下列推理是归纳推理的是（ ）
| A、A，B为定点，动点P满足|PA|+|PB|=2a＞|AB|，得P的轨迹为椭圆 | ||||
| B、科学家利用鱼的沉浮原理制造潜艇 | ||||
C、由圆x2+y2=r2的面积πr2，猜出椭圆
| ||||
| D、由a1=1，an=3n-1，求出S1，S2，S3，猜想出数列的前n项和Sn的表达式 |
考点：归纳推理
专题：归纳法
分析：A．用的是“演绎法”得出点P的轨迹；
B．用的是“类比推理”；
C．用的是“类比推理”；
D．用的是“归纳推理”．
B．用的是“类比推理”；
C．用的是“类比推理”；
D．用的是“归纳推理”．
解答：
解：A．用的是“演绎法”得出点P的轨迹；
B．用的是“类比推理”；
C．用的是“类比推理”；
D．用的是“归纳推理”．
故选：D．
B．用的是“类比推理”；
C．用的是“类比推理”；
D．用的是“归纳推理”．
故选：D．
点评：本题考查了解题方法，属于基础题．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
函数f（x）的导函数f′（x）=2x+2，则f（x）可能是（ ）
| A、f（x）=x2+2 |
| B、f（x）=2x+2 |
| C、f（x）=x2+2x-3 |
| D、f（x）=x3+x2 |
复数
等于（ ）
| 2+3i |
| 3-2i |
| A、-i | B、i |
| C、12-13i | D、12+13i |
化简
+
+
-
=（ ）
| AB |
| BD |
| CA |
| CD |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f（x）=x（x-a）（x-b）的导函数为f′（x），且f′（0）=4，则a2+2b2的最小值为（ ）
| A、1 | ||
| B、4 | ||
C、2
| ||
D、8
|
已知x=
与x=
为函数f（x）=3sin（ωx+
）的两条相邻对称轴，则ω=（ ）
| π |
| 4 |
| 3π |
| 4 |
| π |
| 6 |
| A、1 | B、2 | C、±1 | D、±2 |
若点P在曲线y=x3-x上移动，则过P点的切线的倾斜角的取值范围是（ ）
| A、[0，π） | ||||||
B、（0，
| ||||||
C、[0，
| ||||||
D、[0，
|
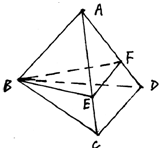已知正三棱锥A-BCD中，底面边长为a，侧棱长为2a，过B点作与则棱AC、AD相交的截面BEF，在这个截面三角形中，求：