题目内容
已知数列{an}满足:a1+a2+…+an=n-an,其中n∈N*.
(1)求证:数列{an-1}是等比数列;
(2)令bn=(2-n)(an-1),求数列{bn}的最大项.
(1)求证:数列{an-1}是等比数列;
(2)令bn=(2-n)(an-1),求数列{bn}的最大项.
考点:等比关系的确定,数列的函数特性
专题:计算题,转化思想
分析:(1)利用等比数列的定义证明数列{an-1}为等比数列并求得通项公式;
(2)由(1)求得数列{bn}的通项公式,根据通项公式分析求解数列{bn}的最大项.
(2)由(1)求得数列{bn}的通项公式,根据通项公式分析求解数列{bn}的最大项.
解答:
(1)证明:当n=1时,a1=1-a1,∴a1=
,
又a1+a2+…+an+1=n+1-an+1
∴an+1=1-an+1+an,即2an+1=1+an,∴an+1-1=
(an-1),又a1-1=-
,
∴数列{an-1}是首项为-
,公比为
的等比数列;
(2)解:由(1)知,an-1=(-
)×(
)n-1=-(
)n,
∴bn=(2-n)•(an-1)=
,
∴bn+1-bn=
-
=
,
当n<3时,bn+1-bn>0,即b1<b2<b3,当n=3时,b4=b3,
当n>3时,bn+1-bn<0,即b4>b5>b6>…;
∴数列{bn}的最大项为b4=b3=
.
| 1 |
| 2 |
又a1+a2+…+an+1=n+1-an+1
∴an+1=1-an+1+an,即2an+1=1+an,∴an+1-1=
| 1 |
| 2 |
| 1 |
| 2 |
∴数列{an-1}是首项为-
| 1 |
| 2 |
| 1 |
| 2 |
(2)解:由(1)知,an-1=(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴bn=(2-n)•(an-1)=
| n-2 |
| 2n |
∴bn+1-bn=
| n+1-2 |
| 2n+1 |
| n-2 |
| 2n |
| 3-n |
| 2n+1 |
当n<3时,bn+1-bn>0,即b1<b2<b3,当n=3时,b4=b3,
当n>3时,bn+1-bn<0,即b4>b5>b6>…;
∴数列{bn}的最大项为b4=b3=
| 1 |
| 8 |
点评:本题考查了等比数列的判定及应用,考查了学生的推理论证能力及运算能力,解题的关键是求得数列{an-1}的通项公式及数列{bn}的通项公式,解题要认真细心.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知函数f(x)=x(x-a)(x-b)的导函数为f′(x),且f′(0)=4,则a2+2b2的最小值为( )
| A、1 | ||
| B、4 | ||
C、2
| ||
D、8
|
下列命题中,假命题的是( )
A、?x0∈R,sinx0+
| ||
| B、?x∈[0,+∞),ex-x>0 | ||
| C、?x0∈(0,+∞),lgx0=-1 | ||
| D、?x∈(-∞,0],2x2-3x-2>0 |
已知a,b表示不同的直线,α,β表示不同的平面,则下列命题正确的是( )
| A、若a∥α,b∥β,α∥β,则a∥b |
| B、若a∥b,a?α,b?β,则α∥β |
| C、若a∥b,a?α,b?α,则a∥α |
| D、若α∩β=a,b∥β,则a∥b |
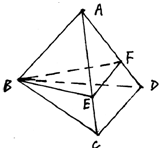 已知正三棱锥A-BCD中,底面边长为a,侧棱长为2a,过B点作与则棱AC、AD相交的截面BEF,在这个截面三角形中,求:
已知正三棱锥A-BCD中,底面边长为a,侧棱长为2a,过B点作与则棱AC、AD相交的截面BEF,在这个截面三角形中,求: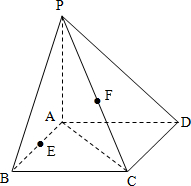 已知PA⊥平面ABCD,四边形ABCD为正方形,PA=AB=4,E、F分别为AB、PC的中点.
已知PA⊥平面ABCD,四边形ABCD为正方形,PA=AB=4,E、F分别为AB、PC的中点. 已知三棱锥A-BCD中,侧棱长和底面边长均相等,E为侧棱AB的中点,求证:
已知三棱锥A-BCD中,侧棱长和底面边长均相等,E为侧棱AB的中点,求证: