题目内容
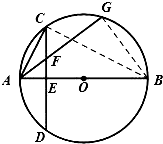 已知,AB为圆O的直径,CD为垂直AB的一条弦,垂足为E,弦AG交CD于F.
已知,AB为圆O的直径,CD为垂直AB的一条弦,垂足为E,弦AG交CD于F.(1)求证:E、F、G、B四点共圆;
(2)若GF=2FA=4,求线段AC的长.
考点:与圆有关的比例线段
专题:计算题,证明题,立体几何
分析:(1)连结BG,由AB为直径可知∠AGB=90°,又CD⊥AB,由此能证明E、F、G、B四点共圆;
(2)连结BC,由E、F、G、B四点共圆,运用切割线定理,得AF•AG=AE•BA,再由直角三角形ABC中的射影定理,得AC2=AE•BA,代入数据,即可求出线段AC的长.
(2)连结BC,由E、F、G、B四点共圆,运用切割线定理,得AF•AG=AE•BA,再由直角三角形ABC中的射影定理,得AC2=AE•BA,代入数据,即可求出线段AC的长.
解答:
(1)证明:如图,连结BG,
由AB为直径可知∠AGB=90°
又CD⊥AB,所以∠BEF=∠AGB=90°,
因此E、F、G、B四点共圆.
(2)解:连结BC,由E、F、G、B四点共圆,
所以AF•AG=AE•BA,
在Rt△ABC中,AC2=AE•BA,
由于GF=2FA=4,得AF=2,FG=4,即有AG=6,
所以AC2=2×6,
故AC=2
.
由AB为直径可知∠AGB=90°

又CD⊥AB,所以∠BEF=∠AGB=90°,
因此E、F、G、B四点共圆.
(2)解:连结BC,由E、F、G、B四点共圆,
所以AF•AG=AE•BA,
在Rt△ABC中,AC2=AE•BA,
由于GF=2FA=4,得AF=2,FG=4,即有AG=6,
所以AC2=2×6,
故AC=2
| 3 |
点评:本题考查四点共圆的证明,考查运用圆的切割线定理和直角三角形的射影定理,求线段长,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
二直线mx+3y+3=0,2x+(m-1)y+2=0平行,则实数m的值为( )
| A、3或-2 | B、-3或2 |
| C、3 | D、-2 |
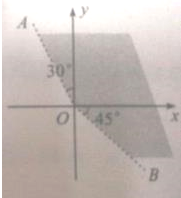 如图,终边落在OA位置的角α的集合是
如图,终边落在OA位置的角α的集合是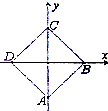 如图,正方形ABCD的边长为2,分别以DB,AC所在直线为x,y轴建立直角坐标系,用斜二测画法得到水平放置的正方形ABCD的直观图A′B′C′D′,则四边形A′B′C′D′的面积为
如图,正方形ABCD的边长为2,分别以DB,AC所在直线为x,y轴建立直角坐标系,用斜二测画法得到水平放置的正方形ABCD的直观图A′B′C′D′,则四边形A′B′C′D′的面积为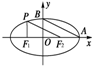 如图,椭圆的中心在原点,焦点F1、F2在x轴上,A、B是椭圆的顶点,P是椭圆上一点,且
如图,椭圆的中心在原点,焦点F1、F2在x轴上,A、B是椭圆的顶点,P是椭圆上一点,且