题目内容
已知向量
=(x,-1),
=(2,y),其中x随机选自集合{-1,1,3},y随机选自集合{-2,2,6},
(Ⅰ)求
∥
的概率;
(Ⅱ)求
⊥
的概率.
| a |
| b |
(Ⅰ)求
| a |
| b |
(Ⅱ)求
| a |
| b |
考点:古典概型及其概率计算公式
专题:平面向量及应用,概率与统计
分析:列举出基本事件空间包含的基本事件个数:
(Ⅰ)由于
∥
等价于
=λ
,即xy+2=0,即 xy=-2,满足xy=-2的(x,y)共有2个,由此求得
∥
的概率.
(Ⅱ)由于
⊥
等价于
•
=0,即2x-y=0,即 y=2x,满足y=2x 的(x,y)共有3个,由此求得
⊥
的概率.
(Ⅰ)由于
| a |
| b |
| a |
| b |
| a |
| b |
(Ⅱ)由于
| a |
| b |
| a |
| b |
| a |
| b |
解答:
解:则基本事件空间包含的基本事件有:(-1,-2),(-1,2),(-1,6),
(1,-2),(1,2),(1,6),(3,-2),(3,2),(3,6),共9种.…(4分)
(Ⅰ)设“
∥
”事件为A,则xy=-2.
事件A包含的基本事件有(-1,2),(1,-2)共2种.
∴
∥
的概率为P(A)=
. …(8分)
(Ⅱ)设“
⊥
”事件为B,则y=2x.
事件A包含的基本事件有(-1,-2),(1,2),(3,6)共3种.
∴
⊥
的概率为P(B)=
=
. …(12分)
(1,-2),(1,2),(1,6),(3,-2),(3,2),(3,6),共9种.…(4分)
(Ⅰ)设“
| a |
| b |
事件A包含的基本事件有(-1,2),(1,-2)共2种.
∴
| a |
| b |
| 2 |
| 9 |
(Ⅱ)设“
| a |
| b |
事件A包含的基本事件有(-1,-2),(1,2),(3,6)共3种.
∴
| a |
| b |
| 3 |
| 9 |
| 1 |
| 3 |
点评:本题主要考查古典概型及其概率计算公式的应用,两个向量平行和垂直的性质,属于基础题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
已知一组数据a1,a2,a3,…,an的平均数为
,标准差为s,则-2a1+3,-2a2+3,-2a3+3,…,-2an+3的平均数和标准差分别是( )
. |
| x |
A、
| ||
B、-2
| ||
C、-2
| ||
D、-2
|
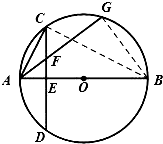 已知,AB为圆O的直径,CD为垂直AB的一条弦,垂足为E,弦AG交CD于F.
已知,AB为圆O的直径,CD为垂直AB的一条弦,垂足为E,弦AG交CD于F.