题目内容
在△ABC中，a、b、c分别为内角A、B、C的对边，且
+
=1，
（1）求角A的大小；
（2）若
=
，a=
，求b的值．
| c |
| a+b |
| b |
| a+c |
（1）求角A的大小；
（2）若
| c |
| b |
2+
| ||
| 4 |
| 15 |
考点：正弦定理,余弦定理
专题：计算题,三角函数的求值
分析：（1）把已知等式化简整理，并利用余弦定理可取的cosA的值，进而求得A的值．
（2）根据b，c的比例关系设出b，c的值，进而根据余弦定理建立方程求得t，最后求得b．
（2）根据b，c的比例关系设出b，c的值，进而根据余弦定理建立方程求得t，最后求得b．
解答：
解：（1）∵且
+
=1，
∴a2+ab+ac+bc=c2+ac+b2+ab
∴b2+c2-a2=bc
∴2bccosA=ab
∴cosA=
，
∵0°＜∠A＜180°
∴∠A=60°
（2）∵
=
，
∴令b=4t，c=（2+
）t，
cosA=
=
=
，
解得t=1
∴b=4．
| c |
| a+b |
| b |
| a+c |
∴a2+ab+ac+bc=c2+ac+b2+ab
∴b2+c2-a2=bc
∴2bccosA=ab
∴cosA=
| 1 |
| 2 |
∵0°＜∠A＜180°
∴∠A=60°
（2）∵
| c |
| b |
2+
| ||
| 4 |
∴令b=4t，c=（2+
| 3 |
cosA=
| b2+c2-a2 |
| 2bc |
16t2+(7+4
| ||
8(2+
|
| 1 |
| 2 |
解得t=1
∴b=4．
点评：本题主要考查了余弦定理的运用．在解三角形的过程中往往借助正弦定理、余弦定理转换边和角的问题．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
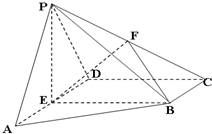已知在四棱锥P-ABCD中，AD∥BC，AD⊥CD，PA=PD=AD=2BC=2CD，E，F分别是AD，PC的中点．
