Question

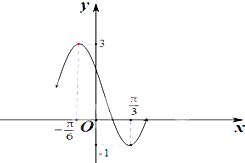已知函数g（x）=Acos（ωx+φ）+B（A＞0，ω＞0，|φ|＜

π

2

）的部分图象如图所示
（1）将函数g（x）的图象保持纵坐标不变，横坐标向右平移

π

3

个单位后得到函数f（x）的图象，求函数f（x）的最大值及最小正周期；
（2）求使f（x）≥2的x的取值范围的集合．

Answer 1

考点：函数y=Asin（ωx+φ）的图象变换

专题：三角函数的图像与性质

分析：（1）由图象求出A，B和半周期，则周期可求，代入周期公式得到ω的值，由五点作图的第一点求得φ的值，则函数g（x）的解析式可求，平移后得到f（x）的解析式，则函数f（x）的最大值及最小正周期可求；
（2）直接解三角不等式求得使f（x）≥2的x的取值范围的集合．

解答： 解：（1）由图可知，A=

3-1

2

=2，则B=3-2=1，

T

2

=

π

3

-(-

π

6

)=

π

2

，
∴T=π，则ω=

2π

π

=2．
由五点作图的第一点得，2×(-

π

6

)+φ=0，得φ=

π

3

．
∴g（x）=2cos（2x+

π

3

）+1，
则g（x）=2cos（2x-

π

3

）+1．
f（x）_max=3，T=

2π

2

=π；
（2）由f（x）≥2，得：
2cos（2x-

π

3

）+1≥2，即cos（2x-

π

3

）≥

1

2

，
∴-

π

3

+2kπ≤2x-

π

3

≤

π

3

+2kπ，
解得：kπ≤x≤kπ+

π

3

，k∈Z．
∴使f（x）≥2的x的取值范围的集合是[kπ，kπ+

π

3

]，k∈Z．

点评：本题考查y=Asin（ωx+φ）型函数图象的求法，训练了三角不等式的解法，是中档题．