题目内容
已知函数f（x）=|2x+a|在[3，+∞）单调递增，求a的取值范围．
考点：带绝对值的函数
专题：选作题,函数的性质及应用
分析：函数f（x）=|2x+a|的零点是-
，利用函数f（x）=|2x+a|在[3，+∞）单调递增，可得-
≤3，即可求a的取值范围．
| a |
| 2 |
| a |
| 2 |
解答：
解：函数f（x）=|2x+a|的零点是-
，
∵函数f（x）=|2x+a|在[3，+∞）单调递增，
∴-
≤3，
∴a≥-6．
| a |
| 2 |
∵函数f（x）=|2x+a|在[3，+∞）单调递增，
∴-
| a |
| 2 |
∴a≥-6．
点评：本题考查带绝对值的函数，考查函数的单调性，考查学生的计算能力，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
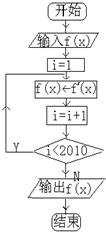
程序框图如图所示，该程序运行后输出的S的值是（ ）
A、
| ||
| B、-3 | ||
C、-
| ||
| D、2 |
设集合A={x|x2-5x+4＜0}，B={y|-1＜y＜3}，则A∩（∁RB）=（ ）
| A、（1，4） |
| B、[3，4） |
| C、（1，3） |
| D、（1，2）∪（3，4） |
集合A={x|y=ln（-x2+2x+3）}，B={y|y=ex}，则A∩B=（ ）
| A、{x|-1＜x＜0} |
| B、{x|0＜x＜3} |
| C、{x|x＞-1} |
| D、{x|x＜3} |
已知互不垂直的平面α，β，γ和互不相同的直线a，b，l，则下列命题正确的个数是（ ）
①
⇒a⊥α
②
⇒α∥β
③
⇒a，b异面
④
⇒a∥b．
①
|
②
|
③
|
④
|
| A、1个 | B、2个 | C、3个 | D、4个 |
设函数f（x）=x•ecosx（x∈[-π，π]）的图象大致是（ ）
A、 |
B、 |
C、 |
D、 |