题目内容
设集合A={x|x2-5x+4＜0}，B={y|-1＜y＜3}，则A∩（∁RB）=（ ）
| A、（1，4） |
| B、[3，4） |
| C、（1，3） |
| D、（1，2）∪（3，4） |
考点：交、并、补集的混合运算
专题：集合
分析：求出集合A，B，根据集合的基本运算进行求解即可．
解答：
解：A={x|x2-5x+4＜0}={x|1＜x＜4}，
∵B={y|-1＜y＜3}，
∴∁RB={x|x≥3或x≤-1}，
则A∩（∁RB）={x|3≤x＜4}，
故选：B．
∵B={y|-1＜y＜3}，
∴∁RB={x|x≥3或x≤-1}，
则A∩（∁RB）={x|3≤x＜4}，
故选：B．
点评：本题主要考查集合的基本运算，要求熟练掌握集合的交并补运算，比较基础．
练习册系列答案
同步练习强化拓展系列答案
相关题目
直线l1：ax+（1-a）y=0，l2：（a-1）x+3y=2互相垂直，则a的值为（ ）
| A、-3 | B、1 |
| C、1或-3 | D、1或3 |
若
=-1，则f′（x0）等于（ ）
| lim |
| k→0 |
| f(x0-k)-f(x0) |
| k |
| A、-1 | B、1 | C、0 | D、无法确定 |
若a=30.2，b=logπ3，c=log3cos
π，则（ ）
| ||
| 4 |
| A、b＞c＞a |
| B、b＞a＞c |
| C、a＞b＞c |
| D、c＞a＞b |
集合A={x|{y=
}，B={y|y=x2-2x}，求A∩B=（ ）
| x2-4 |
| A、[-1，+∞） |
| B、[2，+∞） |
| C、（-∞，-2]∪[2，+∞） |
| D、（-∞，-2]∪[-1，+∞） |
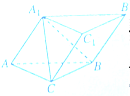如图，在三棱柱ABC-A1B1C1中，四边形A1ABB1为菱形，四边形BCC1B1为矩形，若AB⊥BC且AB=4，BC=3，∠A1AB=60°