题目内容
已知互不垂直的平面α,β,γ和互不相同的直线a,b,l,则下列命题正确的个数是( )
①
⇒a⊥α
②
⇒α∥β
③
⇒a,b异面
④
⇒a∥b.
①
|
②
|
③
|
④
|
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:直线与平面平行的判定
专题:空间位置关系与距离
分析:由直线与平面垂直的判定定理,得①正确;由平面与平面平行的判定定理,得②正确;由异面直线的判定定理,得③正确;由平面两直线平行的判定定理,得④正确.
解答:
解:由互不垂直的平面α,β,γ和互不相同的直线a,b,l,知:
①
⇒a⊥α,由直线与平面垂直的判定定理,得①正确;
②
⇒α∥β,由平面与平面平行的判定定理,得②正确;
③
⇒a,b异面,由异面直线的判定定理,得③正确;
④
⇒a∥b,由平面两直线平行的判定定理,得④正确.
故选:D.
①
|
②
|
③
|
④
|
故选:D.
点评:本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
若a=30.2,b=logπ3,c=log3cos
π,则( )
| ||
| 4 |
| A、b>c>a |
| B、b>a>c |
| C、a>b>c |
| D、c>a>b |
集合A={x|{y=
},B={y|y=x2-2x},求A∩B=( )
| x2-4 |
| A、[-1,+∞) |
| B、[2,+∞) |
| C、(-∞,-2]∪[2,+∞) |
| D、(-∞,-2]∪[-1,+∞) |
 某程序的框图如图所示,执行该程序,若输入的p为l6,则输出的n的值为
某程序的框图如图所示,执行该程序,若输入的p为l6,则输出的n的值为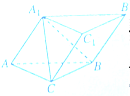 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3,∠A1AB=60°
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3,∠A1AB=60° 如图,在三棱锥P-ABC中,已知平面PBC⊥平面ABC.
如图,在三棱锥P-ABC中,已知平面PBC⊥平面ABC.