题目内容
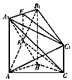
 如图,在几何体ABC-A1B1C1中,点A1,B1,C1在平面ABC内的正投影分别为A,B,C,且AB⊥BC,E为AB1中点,AB=AA1=BB1=2CC1.
如图,在几何体ABC-A1B1C1中,点A1,B1,C1在平面ABC内的正投影分别为A,B,C,且AB⊥BC,E为AB1中点,AB=AA1=BB1=2CC1.(Ⅰ)求证;CE∥平面A1B1C1,
(Ⅱ)求证:平面AB1C1⊥平面A1BC.
考点:平面与平面垂直的判定,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)取A1B1中点F,连接EF,FC,证明CE∥平面A1B1C1,只需证明CE∥C1F;
(Ⅱ)证明BC⊥AB1,AB1⊥A1B,可得AB1⊥平面A1BC,即可证明平面AB1C1⊥平面A1BC.
(Ⅱ)证明BC⊥AB1,AB1⊥A1B,可得AB1⊥平面A1BC,即可证明平面AB1C1⊥平面A1BC.
解答:
 证明:(Ⅰ)∵点A1,B1,C1在平面ABC内的正投影分别为A,B,C,
证明:(Ⅰ)∵点A1,B1,C1在平面ABC内的正投影分别为A,B,C,
∴AA1∥BB1∥CC1,
取A1B1中点F,连接EF,FC,则EF∥
A1A,EF=
A1A
∵AA1=4,CC1=2,∴CC1∥
A1A,CC1=
A1A,
∴CC1∥EF,CC1=EF,
∴四边形EFC1C为平行四边形,
∴CE∥C1F,
∵CE?平面A1B1C1,C1F?平面A1B1C1,
∴CE∥平面A1B1C1;
(Ⅱ)∵BB1⊥平面ABC,∴BB1⊥BC,
∵AB⊥BC,
∵AB∩BB1=B,
∴BC⊥平面AA1BB1,
∵AB1?平面AA1BB1,
∴BC⊥AB1,
∵AA1=BB1=AB,AA1∥BB1,
∴四边形AA1BB1为正方形,
∴AB1⊥A1B,
∵A1B∩BC=B,
∴AB1⊥平面A1BC,
∴平面AB1C1⊥平面A1BC.
 证明:(Ⅰ)∵点A1,B1,C1在平面ABC内的正投影分别为A,B,C,
证明:(Ⅰ)∵点A1,B1,C1在平面ABC内的正投影分别为A,B,C,∴AA1∥BB1∥CC1,
取A1B1中点F,连接EF,FC,则EF∥
| 1 |
| 2 |
| 1 |
| 2 |
∵AA1=4,CC1=2,∴CC1∥
| 1 |
| 2 |
| 1 |
| 2 |
∴CC1∥EF,CC1=EF,
∴四边形EFC1C为平行四边形,
∴CE∥C1F,
∵CE?平面A1B1C1,C1F?平面A1B1C1,
∴CE∥平面A1B1C1;
(Ⅱ)∵BB1⊥平面ABC,∴BB1⊥BC,
∵AB⊥BC,
∵AB∩BB1=B,
∴BC⊥平面AA1BB1,
∵AB1?平面AA1BB1,
∴BC⊥AB1,
∵AA1=BB1=AB,AA1∥BB1,
∴四边形AA1BB1为正方形,
∴AB1⊥A1B,
∵A1B∩BC=B,
∴AB1⊥平面A1BC,
∴平面AB1C1⊥平面A1BC.
点评:本题考查线面平行,面面垂直,考查学生分析解决问题的能力,掌握线面平行、面面垂直的判定定理是关键.

练习册系列答案
相关题目
函数f(x)=
在[-2,2]上的最大值为1,则实数a的取值范围是( )
|
| A、[0,+∞) |
| B、[0,e] |
| C、(-∞,0] |
| D、(-∞,e] |
与60°角终边相同的角的集合可以表示为( )
A、{α|α=k•360°+
| ||
| B、{α|α=2kπ+60°,k∈Z} | ||
| C、{α|α=k•180°+60°,k∈Z} | ||
D、{α|α=2kπ+
|
正方体ABCD-A1B1C1D1中,M,N分别为AB,DC中点,则直线MC与D1N所成角的余弦值为( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
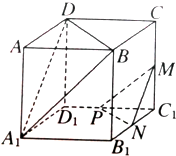 在如图所示的正方体ABCD-A1B1C1D1中.
在如图所示的正方体ABCD-A1B1C1D1中.