题目内容
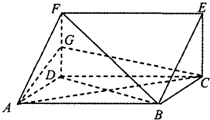已知三棱柱ADF-BCE中，DF⊥平面ABCD，AD=DC，G是DF的中点（Ⅰ）求证：BF∥平面ACG；
（Ⅱ）求证：平面ACG⊥平面BDF．
考点：平面与平面垂直的判定,直线与平面平行的判定
专题：综合题,空间位置关系与距离
分析：（I）设AC、BD交于点O，连接OG．根据三角形中位线定理证出OG∥BF，再结合线面平行的判定定理，可得BF∥平面ACG；
（II）证明AC⊥平面BDF，即可证明平面ACG⊥平面BDF．
（II）证明AC⊥平面BDF，即可证明平面ACG⊥平面BDF．
解答：
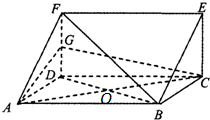证明：（Ⅰ）设AC、BD相交于点O，连结OG，
∵AD=DC∴ABCD为菱形，
∴O为BD的中点，
∵G是FD的中点，
∴OG∥BF；
又∵OG?平面AGCBF?平面AGC，
∴BF∥平面ACG…（6分）
（Ⅱ）∵ABCD为菱形，
∴AC⊥BD，
又∵DF⊥平面ABCDAC?平面ABCD，
∴DF⊥AC；
又∵BD∩DF=DBD、DF?平面BDF，
∴AC⊥平面BDF，
又∵AC?平面ACG，
∴平面ACG⊥平面BDF．…（12分）
证明：（Ⅰ）设AC、BD相交于点O，连结OG，∵AD=DC∴ABCD为菱形，
∴O为BD的中点，
∵G是FD的中点，
∴OG∥BF；
又∵OG?平面AGCBF?平面AGC，
∴BF∥平面ACG…（6分）
（Ⅱ）∵ABCD为菱形，
∴AC⊥BD，
又∵DF⊥平面ABCDAC?平面ABCD，
∴DF⊥AC；
又∵BD∩DF=DBD、DF?平面BDF，
∴AC⊥平面BDF，
又∵AC?平面ACG，
∴平面ACG⊥平面BDF．…（12分）
点评：本题给出特殊的三棱柱，求证线面平行、平面与平面垂直，着重考查了直线与平面平行的判定和平面与平面垂直的判定等知识，属于中档题．
练习册系列答案
小学夺冠AB卷系列答案
相关题目