题目内容
①一个命题的逆命题为真,它的否命题也一定为真;
②在△ABC中,“∠B=60°”是“∠A,∠B,∠C三个角成等差数列”的充要条件;
③
是
的充要条件;
④“am2<bm2”是“a<b”的充分必要条件;
⑤△ABC中,“sinA<sinB”是“∠A<∠B”的充要条件;
以上说法中,判断错误的有 .
②在△ABC中,“∠B=60°”是“∠A,∠B,∠C三个角成等差数列”的充要条件;
③
|
|
④“am2<bm2”是“a<b”的充分必要条件;
⑤△ABC中,“sinA<sinB”是“∠A<∠B”的充要条件;
以上说法中,判断错误的有
考点:命题的真假判断与应用
专题:简易逻辑
分析:根据题意,依次分析4个命题:对于①,由一个命题的逆命题与其否命题互为逆否命题,而互为逆否命题的两个命题同真同假,结合题意可得①正确,对于②,由∠B=60°,易得∠A+∠C=2∠B,可得∠A,∠B,∠C三个角成等差数列;反之由∠A,∠B,∠C三个角成等差数列,可得∠A+∠C=2∠B,又由∠A+∠B+∠C=180°,则∠B=60°,综合可得②正确;对于③举出反例,x=
,y=
,可得
是
的不必要条件,即可得③错误;对于④,举出反例,m=0,易得“am2<bm2”是“a<b”的不必要条件,可得④错误;综合可得答案;对于⑤,对B分类讨论,能够得到sinA<sinB⇒∠A<∠B,∠A<∠B⇒sinA<sinB,命题⑤正确.
| 1 |
| 2 |
| 9 |
| 2 |
|
|
解答:
解:①、一个命题的逆命题与其否命题互为逆否命题,则若其逆命题为真,其否命题也一定为真,①正确;
②、若∠B=60°,则∠A+∠C=120°,有∠A+∠C=2∠B,则∠A,∠B,∠C三个角成等差数列,
反之若∠A,∠B,∠C三个角成等差数列,有∠A+∠C=2∠B,又由∠A+∠B+∠C=180°,则∠B=60°,
故在△ABC中,“∠B=60°”是“∠A,∠B,∠C三个角成等差数列”的充要条件,②正确;
③、当x=
,y=
,则满足
,而不满足
,则
是
的不必要条件,③错误;
④、若a<b,当m=0时,有am2=bm2,则“am2<bm2”是“a<b”的不必要条件,④错误;
⑤、△ABC中,若B>A,当B不超过90°时,显然可得出sinB>sinA,当B是钝角时,由于
>π-B>A,可得sin(π-B)=sinB>sinA,即 B>A是sinB>sinA的充分条件,当sinB>sinA时,亦可得B>A,“sinA<sinB”是“∠A<∠B”的充要条件,命题⑤正确.
故答案为③④.
②、若∠B=60°,则∠A+∠C=120°,有∠A+∠C=2∠B,则∠A,∠B,∠C三个角成等差数列,
反之若∠A,∠B,∠C三个角成等差数列,有∠A+∠C=2∠B,又由∠A+∠B+∠C=180°,则∠B=60°,
故在△ABC中,“∠B=60°”是“∠A,∠B,∠C三个角成等差数列”的充要条件,②正确;
③、当x=
| 1 |
| 2 |
| 9 |
| 2 |
|
|
|
|
④、若a<b,当m=0时,有am2=bm2,则“am2<bm2”是“a<b”的不必要条件,④错误;
⑤、△ABC中,若B>A,当B不超过90°时,显然可得出sinB>sinA,当B是钝角时,由于
| π |
| 2 |
故答案为③④.
点评:本题考查命题正误的判断,一般涉及知识点较多;注意合理运用反例,来判断命题的错误,是中档题.

练习册系列答案
相关题目
若原点和点(1,1)都在直线x+y=a的同一侧,则a的取值范围是( )
| A、a<0或a>2 |
| B、0<a<2 |
| C、a=0或a=2 |
| D、0≤a≤2 |
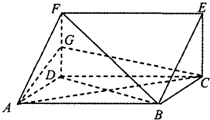 已知三棱柱ADF-BCE中,DF⊥平面ABCD,AD=DC,G是DF的中点
已知三棱柱ADF-BCE中,DF⊥平面ABCD,AD=DC,G是DF的中点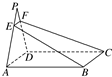 如图所示,四边形ABCD是矩形,P∉平面ABCD,过BC作平面BCFE交AP于E,交DP于F.
如图所示,四边形ABCD是矩形,P∉平面ABCD,过BC作平面BCFE交AP于E,交DP于F.