题目内容
设函数f(x)=
,若f[f(-1)]=2,则实数a= .
|
考点:函数的值
专题:函数的性质及应用
分析:由分段函数的表达式,先求f(-1),再求f[f(-1)],解关于a的方程即可.
解答:
解:f(-1)=2-1=
,
∴f[f(-1)]=f(
)=a+1,
∴a+1=2,
解得a=1,
故答案为:1.
| 1 |
| 2 |
∴f[f(-1)]=f(
| 1 |
| 2 |
∴a+1=2,
解得a=1,
故答案为:1.
点评:本题考查分段函数及应用,考查分段函数值,应注意各段的范围,是一道基础题.

练习册系列答案
相关题目
若原点和点(1,1)都在直线x+y=a的同一侧,则a的取值范围是( )
| A、a<0或a>2 |
| B、0<a<2 |
| C、a=0或a=2 |
| D、0≤a≤2 |
如图给出的是计算
+
+
+…+
的值的一个程序框图,其中判断框中应填入的是( )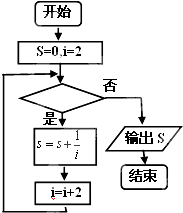
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 100 |

| A、i>100 | B、i≤100 |
| C、i>50 | D、i≤50 |
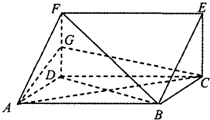 已知三棱柱ADF-BCE中,DF⊥平面ABCD,AD=DC,G是DF的中点
已知三棱柱ADF-BCE中,DF⊥平面ABCD,AD=DC,G是DF的中点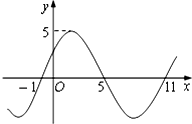 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0≤φ<2π)在R上的部分图象如图所示,则f(2014)=
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0≤φ<2π)在R上的部分图象如图所示,则f(2014)=