题目内容
在△ABC中,A=
,AB=4且S△ABC=
,则BC边的长为 .
| π |
| 3 |
| 3 |
考点:正弦定理
专题:解三角形
分析:由AB,sinA及已知的面积,利用三角形面积公式求出AC的长,再由AB,AC及cosA的值,利用余弦定理即可求出BC的长.
解答:
解:∵A=
,AB=4且S△ABC=
,
∴S△ABC=
AB•AC•sinA,即
=
×4AC×
,
解得:AC=1,
由余弦定理得:BC2=AB2+AC2-2AB•AC•cosA=13,
则BC=
.
故答案为:
.
| π |
| 3 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
解得:AC=1,
由余弦定理得:BC2=AB2+AC2-2AB•AC•cosA=13,
则BC=
| 13 |
故答案为:
| 13 |
点评:此题考查了余弦定理,三角形的面积公式,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
数列{an}的通项公式为an=ncos
,其前n项和为Sn,则S2015等于( )
| nπ |
| 2 |
| A、1002 | B、1004 |
| C、1006 | D、-1008 |
如图给出的是计算
+
+
+…+
的值的一个程序框图,其中判断框中应填入的是( )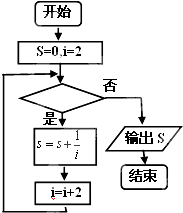
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 100 |

| A、i>100 | B、i≤100 |
| C、i>50 | D、i≤50 |
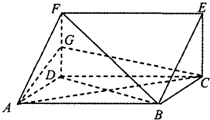 已知三棱柱ADF-BCE中,DF⊥平面ABCD,AD=DC,G是DF的中点
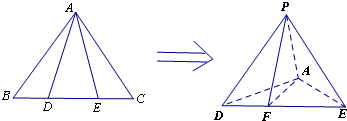
已知三棱柱ADF-BCE中,DF⊥平面ABCD,AD=DC,G是DF的中点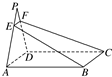 如图所示,四边形ABCD是矩形,P∉平面ABCD,过BC作平面BCFE交AP于E,交DP于F.
如图所示,四边形ABCD是矩形,P∉平面ABCD,过BC作平面BCFE交AP于E,交DP于F.