Question

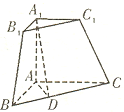三棱锥被平行于底面ABC的平面所截得的几何体如图所示，截面为A₁B₁C₁，直线A₁A⊥平面ABC，A₁A=

3

，AB=AC=2，A₁C₁=1，|

BA

-

AC

|=

3

，D是BC的中点．
（1）证明：平面A₁AD⊥平面BCC₁B₁；
（2）求三棱台ABC-A₁B₁C₁的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,平面与平面垂直的判定

专题：空间位置关系与距离

分析：（1）根据面面垂直的判定定理即可郑明明平面A₁AD⊥平面BCC₁B₁；
（2）根据三棱台的体积公式即可求出三棱台ABC-A₁B₁C₁的体积．

解答： 解：（1）∵A₁ A⊥平面ABC，BC?平面ABC，
∴A₁ A⊥BC．
∵|

BA

-

AC

|=

3

，AB=AC=2
∴∠BAC=60°，∴△ABC为正三角形，即AD⊥BC．
又A₁ A∩AD=A，∴BC⊥平面A₁AD，
∵BC?平面BCC₁B₁，
∴平面A₁ AD⊥平面BCC₁B1．
（2）∵△ABC为边长为2的正三角形，∴△A₁B₁C₁为边长为1的正三角形，
三棱台的高A₁A=

3

，
则S_下=

1

2

×22×

3

2

=

3

，S_上=

1

2

×12×

3

2

=

3

4

则三棱台ABC-A₁B₁C₁的体积V=

1

3

（S_上+S_下+

S上•S下

）•A₁A=

1

3

×(

3

+

3

4

+

3 × 3 4

)×

3

=

7

4

．

点评：本题考查空间面面垂直的判定以及三棱台的体积计算，要求熟练掌握面面垂直的判定定理以及三棱台的体积公式．