题目内容
13.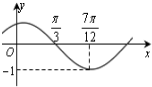 函数f(x)=Asin(ωx+φ)(A>0,ω>0),|φ|<$\frac{π}{2}$)的图象如图所示,则f(0)等于( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0),|φ|<$\frac{π}{2}$)的图象如图所示,则f(0)等于( )| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 根据函数f(x)的图象,求出A、ω与φ的值,写出f(x)的解析式,再求f(0)的值.
解答 解:根据函数f(x)的图象知,函数的最小值为-1,∴A=1;
又$\frac{T}{4}$=$\frac{7π}{12}$-$\frac{π}{3}$=$\frac{π}{4}$,
∴T=π;
根据周期公式可得,$\frac{2π}{ω}$=π,∴ω=2,
∴f(x)=sin(2x+φ);
又函数图象过($\frac{7π}{12}$,-1)
代入可得,sin(2×$\frac{7π}{12}$+φ)=-1,
∴2×$\frac{7π}{12}$+φ=$\frac{3π}{2}$+2kπ,k∈Z,
∴φ=$\frac{π}{3}$+2kπ,k∈Z;
又|φ|<$\frac{π}{2}$,∴φ=$\frac{π}{3}$;
∴f(x)=sin(2x+$\frac{π}{3}$),
∴f(0)=sin$\frac{π}{3}$=$\frac{\sqrt{3}}{2}$.
故选:D.
点评 本题主要考查了由函数的部分图象求函数的解析式,通常是由函数的最值求A,根据周期公式求ω,根据函数的最值点求φ,是基础试题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
4.若十进制数26等于k进制数32,则k等于( )
| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
1.把十进制的数101转化为四进制数,得( )
| A. | 1121(4) | B. | 1211(4) | C. | 1021(4) | D. | 1201(4) |
8.已知函数f(x)=sinωx•cosωx+$\sqrt{3}$cos2ωx-$\frac{\sqrt{3}}{2}$(ω>0),直线x=x1,x=x2是y=f(x)图象的任意两条对称轴,且|x1-x2|的最小值为$\frac{π}{4}$,若关于x的方程f(x)+k=0在区间[0,$\frac{π}{4}$]上有两个不同的实数解,则实数k的取值范围为( )
| A. | (-1,1) | B. | ($\frac{\sqrt{3}}{2}$,1) | C. | (-1,-$\frac{\sqrt{3}}{2}$] | D. | (-1,$\frac{\sqrt{3}}{2}$] |
2.下列函数中,最小正周期为π的偶函数是( )
| A. | y=cos(2x+$\frac{π}{2}$) | B. | y=cos$\frac{x}{2}$ | C. | y=sin(2x-$\frac{π}{2}$) | D. | y=tanx |
3.已知cos(α+2β)=$\frac{1}{5}$,cosα=$\frac{2}{5}$,则tan(α+β)tanβ=( )
| A. | -2 | B. | $\frac{1}{2}$ | C. | 3 | D. | $\frac{1}{3}$ |