题目内容
3.已知cos(α+2β)=$\frac{1}{5}$,cosα=$\frac{2}{5}$,则tan(α+β)tanβ=( )| A. | -2 | B. | $\frac{1}{2}$ | C. | 3 | D. | $\frac{1}{3}$ |
分析 利用“拆角配角”思想把已知变形,得到cos[(α+β)+β]=$\frac{1}{5}$,cos[(α+β)-β]=$\frac{2}{5}$,然后展开两角和与差的余弦,求解sin(α+β)sinβ与cos(α+β)cosβ的值,再由商的关系求得答案.
解答 解:由cos(α+2β)=$\frac{1}{5}$,得cos[(α+β)+β]=$\frac{1}{5}$,
即cos(α+β)cosβ-sin(α+β)sinβ=$\frac{1}{5}$,①
由cosα=$\frac{2}{5}$,得cos[(α+β)-β]=$\frac{2}{5}$,
即cos(α+β)cosβ+sin(α+β)sinβ=$\frac{2}{5}$,②
①+②,得$cos(α+β)cosβ=\frac{3}{10}$,
②-①,得sin(α+β)sinβ=$\frac{1}{10}$.
∴则tan(α+β)tanβ=$\frac{sin(α+β)sinβ}{cos(α+β)cosβ}=\frac{\frac{1}{10}}{\frac{3}{10}}=\frac{1}{3}$.
故选:D.
点评 本题考查两角和与差的余弦,着重考查了“拆角配角”思想的应用,是中档题.

练习册系列答案
相关题目
13.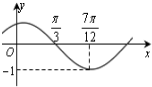 函数f(x)=Asin(ωx+φ)(A>0,ω>0),|φ|<$\frac{π}{2}$)的图象如图所示,则f(0)等于( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0),|φ|<$\frac{π}{2}$)的图象如图所示,则f(0)等于( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0),|φ|<$\frac{π}{2}$)的图象如图所示,则f(0)等于( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0),|φ|<$\frac{π}{2}$)的图象如图所示,则f(0)等于( )| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |