题目内容

3．用分析法证明：当x≥4时，$\sqrt{x-3}$+$\sqrt{x-2}$＞$\sqrt{x-4}$+$\sqrt{x-1}$．

分析 分析使不等式$\sqrt{x-3}$+$\sqrt{x-2}$＞$\sqrt{x-4}$+$\sqrt{x-1}$成立的充分条件，一直分析到使不等式成立的充分条件显然具备，从而不等式得证．

解答 证明：当x≥4时
要证$\sqrt{x-3}+\sqrt{x-2}＞\sqrt{x-4}+\sqrt{x-1}$
只需证${（\sqrt{x-3}+\sqrt{x-2}）^2}＞{（\sqrt{x-4}+\sqrt{x-1}）^2}$------------（2分）
只需证$x-3+2\sqrt{（x-3）（x-2）}+x-2＞x-4+2\sqrt{（x-4）（x-1）}+x-1$-----------（5分）
即证$\sqrt{（x-3）（x-2）}＞\sqrt{（x-4）（x-1）}$
只需证x2-5x+6＞x2-5x+4
即证6＞4
显然上式成立，------------------------（9分）
所以原不等式成立，即$\sqrt{x-3}-\sqrt{x-1}＞\sqrt{x-4}-\sqrt{x-2}$------------（10分）

点评 本题主要考查利用分析法证明不等式，利用用分析法证明不等式的关键是寻找使不等式成立的充分条件，直到使不等式成立的充分条件已经显然具备为止，属于中档题．

练习册系列答案
相关题目
13．设点P（m，n）在圆x2+y2=2上，l是过点P的圆的切线，切线l与函数y=x2+x+k（k∈R）的图象交于A，B两点，点O是坐标原点．
（I）若k=-2，点P恰好是线段AB的中点，求点P的坐标；
（Ⅱ）是否存在实数k，使得以AB为底边的等腰△OAB恰有三个？若存在，求出k的取值范围；若不存在，说明理由．
14．若{an}是正项递增等比数列，Tn表示其前n项之积，且T9=T19，则当Tn取最小值时，n的值为（　　）
A．9B．14C．19D．24
11．函数y=3sin（2x+$\frac{π}{4}$）的图象向左平移φ（0＜φ＜$\frac{π}{2}$）个单位后，所得到函数图象关于原点对称，则φ=$\frac{3π}{8}$．
18．已知点A是抛物线M：y2=2px（p＞0）与圆C：x2+（y-4）2=a2在第一象限的公共点，且点A到抛物线M焦点F的距离为a，若抛物线M上一动点到其准线与到点C的距离之和的最小值为2a，O为坐标原点，则直线OA被圆C所截得的弦长为（　　）
A．2B．2$\sqrt{3}$C．$\frac{7\sqrt{2}}{3}$D．$\frac{7\sqrt{2}}{6}$
8．已知椭圆C1：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b≥1}）$的离心率$\frac{{\sqrt{2}}}{2}$，其右焦点到直线2ax+by-$\sqrt{2}$=0的距离为$\frac{{\sqrt{2}}}{3}$．
（I）求椭圆C1的方程；
（Ⅱ）过点P$（{0，-\frac{1}{3}}）$的直线l交椭圆C1于A、B两点．
（i）证明：线段AB的中点G恒在椭圆C2：$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}$=1的内部；
（ii）判断以AB为直径的圆是否恒过定点？若是，求出该定点坐标；若不是，请说明理由．
15．已知a，b＞0，若圆x2+y2=b2与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1有公共点，则该双曲线的离心率的取值范围是（　　）
A．[$\sqrt{2}$，+∞）B．（1，$\sqrt{2}$]C．（1，$\sqrt{3}$）D．（$\sqrt{2}$，2）
12．若双曲线x2+2my2=1的两条渐近线互相垂直，则其一个焦点为（　　）
A．（0，1）B．（-1，0）C．（0，$\sqrt{2}$）D．（-$\sqrt{2}$，0）
13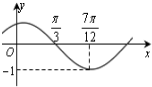．函数f（x）=Asin（ωx+φ）（A＞0，ω＞0），|φ|＜$\frac{π}{2}$）的图象如图所示，则f（0）等于（　　）
A．-$\frac{1}{2}$B．-$\frac{\sqrt{3}}{2}$C．$\frac{1}{2}$D．$\frac{\sqrt{3}}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网