题目内容
18．若a，b，c为Rt△ABC的三边，其中c为斜边，那么当n＞2，n∈N*时，an+bn与cn的大小关系为an+bn＜cn．分析 由题意可得：a2+b2=c2，令$\frac{a}{c}$=cosθ，$\frac{b}{c}$=sinθ，$θ∈（0，\frac{π}{2}）$．当n＞2，n∈N*时，$（\frac{a}{c}）^{n}+（\frac{b}{c}）^{n}$=cosnθ+sinnθ＜cos2θ+sin2θ，即可得出．
解答 解：由题意可得：a2+b2=c2，令$\frac{a}{c}$=cosθ，$\frac{b}{c}$=sinθ，$θ∈（0，\frac{π}{2}）$．
∴cos2θ+sin2θ=1．
∴当n＞2，n∈N*时，$（\frac{a}{c}）^{n}+（\frac{b}{c}）^{n}$=cosnθ+sinnθ＜cos2θ+sin2θ=1．
∴an+bn＜cn，
故答案为：an+bn＜cn．
点评 本题考查了勾股定理、三角函数的单调性、不等式的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
快乐5加2金卷系列答案
相关题目
13．
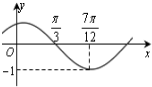函数f（x）=Asin（ωx+φ）（A＞0，ω＞0），|φ|＜$\frac{π}{2}$）的图象如图所示，则f（0）等于（ ）
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0），|φ|＜$\frac{π}{2}$）的图象如图所示，则f（0）等于（ ）| A． | -$\frac{1}{2}$ | B． | -$\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |