题目内容
5.实数m为何值时,复数Z=(m2+5m+6)+(m2-2m-15)i对应的点在:(1)实轴上;
(2)在第一象限;
(3)直线x+y+4=0上.
分析 求出复数对应点的坐标,根据复数的几何意义建立方程或不等式关系进行求解即可.
解答 解:(1)若z对应的点在实轴上,
则m2-2m-15=0,(2分)
解得m=-3或m=5.(5分)
(2)若点在第一象限,则m2+5m+6>0且m2-2m-15>0(2分)
m>5或m<-3(5分)
(3)复数z对应的点为(m2+5m+6,m2-2m-15),
∵z对应的点在直线x+y+4=0上,
∴(m2+5m+6)+(m2-2m-15)+4=0,(2分)
得$m=1,m=-\frac{5}{2}$(5分)
点评 本题主要考查复数的几何意义的应用,根据复数和点的对应关系是解决本题的关键.

练习册系列答案
相关题目
15.已知a,b>0,若圆x2+y2=b2与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1有公共点,则该双曲线的离心率的取值范围是( )
| A. | [$\sqrt{2}$,+∞) | B. | (1,$\sqrt{2}$] | C. | (1,$\sqrt{3}$) | D. | ($\sqrt{2}$,2) |
13.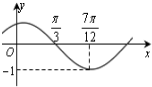 函数f(x)=Asin(ωx+φ)(A>0,ω>0),|φ|<$\frac{π}{2}$)的图象如图所示,则f(0)等于( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0),|φ|<$\frac{π}{2}$)的图象如图所示,则f(0)等于( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0),|φ|<$\frac{π}{2}$)的图象如图所示,则f(0)等于( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0),|φ|<$\frac{π}{2}$)的图象如图所示,则f(0)等于( )| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
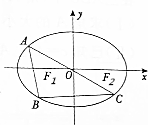 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点F1,F2,过其中两个端点的直线斜率为$\frac{\sqrt{2}}{2}$,过两个焦点和一个顶点的三角形面积为1.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点F1,F2,过其中两个端点的直线斜率为$\frac{\sqrt{2}}{2}$,过两个焦点和一个顶点的三角形面积为1.