题目内容
设α,β(α<β)分别是二次方程ax2+bx+c=0和ax2-bx-c=0的非零根,求证:函数f(x)=
x2+bx+c总在区间(α,β)有零点.
| a |
| 2 |
考点:函数的零点与方程根的关系,函数零点的判定定理
专题:函数的性质及应用
分析:由题意分别表示出f(α),β),得到f(α)f(β)<0,从而问题得证.
解答:
解:由题意可知:aα2+bα+c=0,aβ2-bβ-c=0
bα+c=-aα2,bβ+c=aβ2,f(α)=
α2+bα+c=
α2-aα2=-
α2,
f(β)=
β2+bβ+c=
β2+aβ2=
β2,因为a≠0,α≠0,β≠0,
∴f(α)f(β)<0,即函数f(x)=
x2+bx+c总在区间(α,β)有零点.
bα+c=-aα2,bβ+c=aβ2,f(α)=
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
f(β)=
| a |
| 2 |
| a |
| 2 |
| 3a |
| 2 |
∴f(α)f(β)<0,即函数f(x)=
| a |
| 2 |
点评:本题考查了函数的零点问题,表示出f(α),β),得到f(α)f(β)<0是解题的关键.

练习册系列答案
相关题目
 已知函数y=Asin(ω•x+φ)(A>0,ω>0,|φ|<
已知函数y=Asin(ω•x+φ)(A>0,ω>0,|φ|<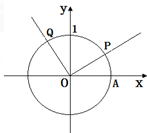 设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且∠AOP=β,β∈(0,
设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且∠AOP=β,β∈(0,