题目内容
18.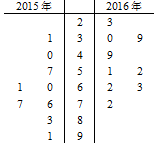 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,它是形成雾霾的原因之一.PM2.5日均值越小,空气质量越好.2012年2月29日,国家环保部发布的《环境空气质量标准》见表:
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,它是形成雾霾的原因之一.PM2.5日均值越小,空气质量越好.2012年2月29日,国家环保部发布的《环境空气质量标准》见表:| PM2.5日均值k(微克) | 空气质量等级 |
| k≤35 | 一级 |
| 35<k≤75 | 二级 |
| k>75 | 超标 |
(Ⅰ)分别求两年样本数据的中位数和平均值,并以此推断2016年11月~12月的空气质量是否比2015年同期有所提高?
(Ⅱ)在2015年的9个样本数据中随机抽取两天的数据,求这两天空气质量均超标的概率?
分析 (Ⅰ)由茎叶图中数据能求出2015,2016两年数据的中位数的平均值,由此得到2016年11月~12月的空气质量比2015年同期有所提高.
(Ⅱ)从2015年的9个数据随机抽取两天的数据,共有36种不同的情况,在这9个数据中,有四个数据是空气质量超标的数据,从中随机抽取两个,有6种不同的情况.由此能求出这两天空气质量均超标的概率.
解答 解:(Ⅰ)由茎叶图中数据可知,2015,2016两年数据的中位数分别为61,51.
2015年数据的平均数为 $\overline{x_1}=\frac{1}{9}(31+40+57+60+61+76+77+83+91)=64$,
2016年数据的平均数为 $\overline{x_2}=\frac{1}{9}(23+30+39+49+51+52+62+63+72)=49$,
∴2016年11月~12月的空气质量比2015年同期有所提高. …6分
(Ⅱ)从2015年的9个数据随机抽取两天的数据,共有36种不同的情况,
而在这9个数据中,有四个数据是空气质量超标的数据,
从中随机抽取两个,有6种不同的情况.
所以所求概率为$P=\frac{6}{36}=\frac{1}{6}$.…12分.
点评 本题考查茎叶图的应用,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.一个圆锥的底面圆半径为3,高为4,则这个圆锥的侧面积为( )
| A. | $\frac{15π}{2}$ | B. | 24π | C. | 15π | D. | 20π |
9.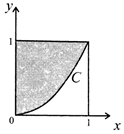 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C的方程为x2-y=0)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C的方程为x2-y=0)的点的个数的估计值为( )
 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C的方程为x2-y=0)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C的方程为x2-y=0)的点的个数的估计值为( )| A. | 5000 | B. | 6667 | C. | 7500 | D. | 7854 |
6.若x0是方程lnx+x-3=0的实数解,则x0属于区间( )
| A. | (1,1.5) | B. | (1.5,2) | C. | (2,2.5) | D. | (2.5,3) |