题目内容
7．在△ABC中，内角A，B，C的对边分别为a，b，c，若bsinB-asinC=0（1）求证：a，b，c成等比数列；
（2）若a=1，c=2，求△ABC的面积S．
分析 （1）由已知及正弦定理可得：b2=ac，从而证明得解．
（2）由已知及余弦定理可求cosB，进而利用同角三角函数基本关系式可求sinB的值，利用三角形面积公式即可计算得解．
解答 （本题满分为12分）
解：（1）证明：∵bsinB-asinC=0，
∴bsinB=asinC，由正弦定理可得：b2=ac，
∴a，b，c成等比数列…6分
（2）∵a=1，c=2，则b2=ac=2，
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{3}{4}$，…8分
∴sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{\sqrt{7}}{4}$，…10分
∴S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}×1×2×\frac{\sqrt{7}}{4}$=$\frac{\sqrt{7}}{4}$…12分
点评 本题主要考查了正弦定理，余弦定理，同角三角函数基本关系式，三角形面积公式在解三角形中的应用，考查了转化思想，属于基础题．
练习册系列答案
相关题目
17．设p：x＜4，q：1＜x＜4，则p是q成立的（ ）
| A． | 充要条件 | B． | 充分不必要条件 | ||
| C． | 必要不充分条件 | D． | 既充分也不必要条件 |
18．
PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，它是形成雾霾的原因之一．PM2.5日均值越小，空气质量越好.2012年2月29日，国家环保部发布的《环境空气质量标准》见表：
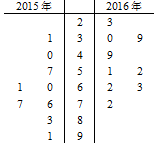
针对日趋严重的雾霾情况，各地环保部门做了积极的治理．马鞍山市环保局从市区2015年11月～12月和2016年11月～12月的PM2.5检测数据中各随机抽取9天的数据来分析治理效果．样本数据如茎叶图所示（十位为茎，个位为叶）
（Ⅰ）分别求两年样本数据的中位数和平均值，并以此推断2016年11月～12月的空气质量是否比2015年同期有所提高？
（Ⅱ）在2015年的9个样本数据中随机抽取两天的数据，求这两天空气质量均超标的概率？
PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，它是形成雾霾的原因之一．PM2.5日均值越小，空气质量越好.2012年2月29日，国家环保部发布的《环境空气质量标准》见表：| PM2.5日均值k（微克） | 空气质量等级 |
| k≤35 | 一级 |
| 35＜k≤75 | 二级 |
| k＞75 | 超标 |
（Ⅰ）分别求两年样本数据的中位数和平均值，并以此推断2016年11月～12月的空气质量是否比2015年同期有所提高？
（Ⅱ）在2015年的9个样本数据中随机抽取两天的数据，求这两天空气质量均超标的概率？
15．已知集合P={x|-1≤x≤1}，M={a}，若P∩M=∅，则a取值范围是（ ）
| A． | （-∞，-1] | B． | [1，+∞） | C． | [-1，1] | D． | （-∞，-1）∪（1，+∞） |
2．已知抛物线C：y2=8x的焦点为F，P为C的准线上一点，Q（在第一象限）是直线PF与C的一个交点，若$\overrightarrow{PQ}=\sqrt{2}\overrightarrow{QF}$，则QF的长为（ ）
| A． | $6-4\sqrt{2}$ | B． | $8-4\sqrt{2}$ | C． | $8+4\sqrt{2}$ | D． | $8±4\sqrt{2}$ |
19．在平面直角坐标系xoy中，双曲线${C_1}：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的渐近线与抛物线${C_2}：{y^2}=2px（{p＞0}）$交于点O，A，B，若△OAB的垂心为C2的焦点，则C1的离心率为（ ）
| A． | $\frac{3}{2}$ | B． | $\sqrt{5}$ | C． | $\frac{{3\sqrt{5}}}{5}$ | D． | $\frac{{\sqrt{5}}}{2}$ |
16．将A，B，C，D这4名同学从左至右随机地排成一排，则“A与B相邻且A与C之间恰好有1名同学”的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{8}$ |