题目内容
设函数f（x）=
+
的最大值为M．
（Ⅰ）求实数M的值；
（Ⅱ）求关于x的不等式|x-1|+|x+2|≤M的解集．
| 2x-4 |
| 5-x |
（Ⅰ）求实数M的值；
（Ⅱ）求关于x的不等式|x-1|+|x+2|≤M的解集．
考点：二维形式的柯西不等式,绝对值不等式
专题：不等式的解法及应用
分析：（Ⅰ）根据函数f（x）=
+
=
•
+
≤
•
=3，求得实数M的值．
（Ⅱ）关于x的不等式即|x-1|+|x+2|≤3，由绝对值三角不等式可得|x-1|+|x+2|≥3，可得|x-1|+|x+2|=3．根据绝对值的意义可得x的范围．
| 2x-4 |
| 5-x |
| 2 |
| x-2 |
| 5-x |
| 2+1 |
| (x-2)+(5-x) |
（Ⅱ）关于x的不等式即|x-1|+|x+2|≤3，由绝对值三角不等式可得|x-1|+|x+2|≥3，可得|x-1|+|x+2|=3．根据绝对值的意义可得x的范围．
解答：
解：（Ⅰ）函数f（x）=
+
=
•
+
≤
•
=3，
当且仅当
=
，即 x=4时，取等号，故实数M=3．
（Ⅱ）关于x的不等式|x-1|+|x+2|≤M，即|x-1|+|x+2|≤3．
由绝对值三角不等式可得|x-1|+|x+2|≥|（x-1）-（x+2）|=3，
∴|x-1|+|x+2|=3．
根据绝对值的意义可得，当且仅当-2≤x≤1时，|x-1|+|x+2|=3，
故不等式的解集为[-2，1]．
| 2x-4 |
| 5-x |
| 2 |
| x-2 |
| 5-x |
| 2+1 |
| (x-2)+(5-x) |
当且仅当
| x-2 |
| 2 |
| 5-x |
| 1 |
（Ⅱ）关于x的不等式|x-1|+|x+2|≤M，即|x-1|+|x+2|≤3．
由绝对值三角不等式可得|x-1|+|x+2|≥|（x-1）-（x+2）|=3，
∴|x-1|+|x+2|=3．
根据绝对值的意义可得，当且仅当-2≤x≤1时，|x-1|+|x+2|=3，
故不等式的解集为[-2，1]．
点评：本题主要考查二维形式的柯西不等式的应用，绝对值的意义，绝对值三角不等式，属于基础题．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
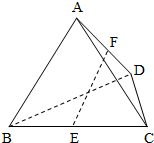在正四面体A-BCD中，E、F分别是BC、AD的中点．
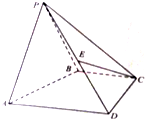如图，四棱锥P-ABCD，底面ABCD为直角梯形，BC∥AD，BC⊥CD，BC=CD=
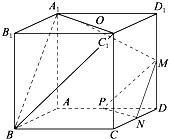如图，在正方体ABCD-A1B1C1D1中，M、N、P分别为所在边的中点，O为面对角线A1C1的中点．